4. Annexe A - Correction des travaux dirigés : logique des propositions▲
4-1. Travaux dirigés 1.2.2▲
Formules bien formées
Les « formules » suivantes sont-elles des formules bien formées ?
| 1 | a ∨ b ∧ c | oui |
| 2 | ¬a ∨ b ∧ c | oui |
| 3 | a ∨ ¬b ∧ c | oui |
| 4 | a¬ ∨ b ∧ c | non |
| 5 | (a) | oui |
| 6 | (a)b | non |
| 7 | ¬b(a) | non |
| 8 | a ∨ ¬(b ∧ c) | oui |
| 9 | a¬(∨b ∧ c) | non |
| 10 | a → b | oui |
| 11 | a ← a | non |
| 12 | a → b ↔ c | oui |
| 13 | a → ¬(b ↔ c) | oui |
| 14 | a¬ → b | non |
| 15 | a ∨ (b ↔ c)¬c → d | non |
| 16 | a ∨ (b ↔ c) → ¬c → d | oui |
Parenthèsage
Explicitez le parenthèsage implicite des formules suivantes :
- a → b → c ≡ ((a → b) → c)
- a ∨ b ∧ c ≡ (a ∨ (b ∧ c))
- a ∨ b ∧ c ↔ d → ¬ e ∨ f ∧ g ≡ ((a ∨ (b ∧ c)) ↔ (d → ((¬e) ∨ (f ∧ g))))
Simplifiez au maximum le parenthèsage des formules suivantes :
- (a) ≡ a
- ((a ∨ b)) ≡ a ∨ b
- ((a) ∧ (b)) ≡ a ∧ b
- (¬(a ∨ b)) ≡ ¬(a ∨ b)
- ¬(((a) ∧ b)) ≡ ¬(a ∧ b)
- a ∨ (b ∧ c) ≡ a ∨ b ∧ c
- (a ∨ b) ∧ c ≡ (a ∨ b) ∧ c
- ((a ∧ b) → c) ≡ a ∧ b → c
- (a ∧ (b → c)) ≡ a ∧ (b → c)
- ((a ∨ b) ∧ c) ↔ e ≡ (a ∨ b) ∧ c ↔ e
- (((a ∨ b) ∧ c) ↔ e) → f ≡ ((a ∨ b) ∧ c ↔ e) → f
- ((a ∧ b) ∨ c) ↔ (e → f) ≡ a ∧ b ∨ c ↔ e → f
- (((a → b) → c) → d) ≡ a → b → c → d
- (a ∧ (b ∧ c)) ≡ a ∧ b ∧ c
- (a → (b → c)) ≡ a → (b → c)
Formalisation d'un énoncé
Traduisez les énoncés suivants en formule logique :
- Quand il fait beau, Jean est heureux ;
il fait soleil ;
donc, Jean est heureux. - Quand il fait beau, Jean est heureux ;
or, Jean est malheureux ;
donc il fait mauvais. - Propositions élémentaires :
b ≡ il fait beau ;
h ≡ Jean est heureux.
Hypothèse 1 : H1 ≡ b → h (Quand il fait beau, Jean est heureux)
Hypothèse 2 : H2 ≡ b (il fait soleil)
Conclusion : C ≡ h (Jean est heureux)
Formulation : H1 ∧ H2 → C ≡ (b → h) ∧ b → h - Propositions élémentaires :
b ≡ il fait beau ;
h ≡ Jean est heureux.
Hypothèse 1 : H1 ≡ b → h (Quand il fait beau, Jean est heureux)
Hypothèse 2 : H2 ≡ ¬b (il fait mauvais)
Conclusion : C ≡ ¬h (Jean est malheureux)
Formulation : H1 ∧ H2 → C ≡ (b → h) ∧ ¬b → ¬h - Propositions élémentaires :
b ≡ il fait beau ;
h ≡ Jean est heureux.
Hypothèse 1 : H1 ≡ b → h (Quand il fait beau, Jean est heureux)
Hypothèse 2 : H2 ≡ ¬h (Jean est malheureux)
Conclusion : C ≡ ¬b (il fait mauvais)
Formulation : H1 ∧ H2 → C ≡ (b → h) ∧ ¬h → ¬b
Ajouter la proposition élémentaire s ≡ il fait soleil produirait une traduction correcte, mais de piètre qualité, car elle aboutirait à une formule dont on ne pourrait rien tirer.
4-2. Travaux dirigés 1.3.5▲
Équivalence de formules
À l'aide d'une table de vérité, vérifiez les deux équivalences de Morgan.
Première équivalence : ¬(A ∨ B) ≡ ¬A ∧ ¬B
| A | B | ¬A | ¬B | A ∨ B | ¬(A ∨ B) | ¬A ∧ ¬B | |
|---|---|---|---|---|---|---|---|
| F | F | T | T | F | T | T | |
| F | T | T | F | T | F | F | |
| T | F | F | T | T | F | F | |
| T | T | F | F | T | F | F |
Les deux formules sont équivalentes (soit toutes les deux fausses, soit toutes les deux vraies) dans toutes les interprétations (quelles que soient les valuations de A et B), il s'agit donc de formules équivalentes.
Deuxième équivalence : ¬(A ∧ B) ≡ ¬A ∨ ¬B
| A | B | ¬A | ¬B | A ∧ B | ¬(A ∧ B) | ¬A ∨ ¬B | |
|---|---|---|---|---|---|---|---|
| F | F | T | T | F | T | T | |
| F | T | T | F | F | T | T | |
| T | F | F | T | F | T | T | |
| T | T | F | F | T | F | F |
Les deux formules sont équivalentes dans toutes les interprétations, elles sont donc équivalentes.
Valeur de formules
-
À l'aide d'une table de vérité, étudiez la validité et la consistance des formules que vous avez trouvées pour l'exercice « Formalisation d'un énoncé » du TD 1.2.2Travaux dirigés (la syntaxe).
b h b → h (b → h) ∧ b (b → h) ∧ b → h F F T F T F T T F T T F F F T T T T T T Premier énoncé : (b → h) ∧ b → h
L'énoncé est vrai dans toutes les interprétations (quelles que soient les valuations de b et h), il est donc valide et donc, à fortiori, consistant.
L'énoncé est vrai dans toutes les interprétations, il est donc valide et donc, à fortiori, consistant.
Deuxième énoncé : (b → h) ∧ ¬h → ¬b
b h b → h ¬h (b → h) ∧ ¬h ¬b (b → h) ∧ ¬h → ¬b F F T T T T T F T T F F T T T F F T F F T T T T F F F T -
À l'aide d'une table de vérité, étudiez la validité et la consistance de la formule suivante :
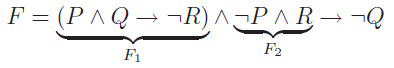
Pour simplifier les écritures, nous désigneront par F1 la formule P ∧Q → ¬R et par F2 la formule ¬P ∧ R.
L'écriture de table de vérité complète devient vite fastidieuse. Aussi est-il souvent intéressant de ne construire qu'une table de vérité partielle. Par exemple, pour la formule précédente, on peut construire une table de vérité partielle comme décrit ci-dessous.
- Si on regarde la table de vérité de l'implication A → B () on se rend compte que quand B est vrai, A → B est vrai quelle que soit la valeur de A.
Or ¬Q vrai est équivalent à Q faux. Donc, quand Q est faux la formule F est vrai.
Ainsi, quand ¬Q est vrai
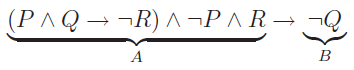 est également vrai, quelle que soit la valeur de (P ∧ Q → ¬R) ∧ ¬P ∧ R.
est également vrai, quelle que soit la valeur de (P ∧ Q → ¬R) ∧ ¬P ∧ R.On en déduit immédiatement les lignes (1), (2), (5) et (6), soit la moitié de la table de vérité !
- De même, si on regarde à nouveau la table de vérité de l'implication A → B () on se rend compte que quand A est faux, A → B est vrai quelle que soit la valeur de B.
Ainsi, quand (P ∧ Q → ¬R) ∧ ¬P ∧ R est faux, la formule
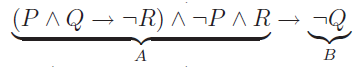 est vrai, quelle que soit la valeur de ¬Q.
est vrai, quelle que soit la valeur de ¬Q.On en déduit immédiatement les lignes (3) et (7).
Ainsi, quand R est faux, la conjonction (P ∧Q → ¬R)∧¬P ∧R est également fausse et la formule F est alors vraie.
Or (P ∧Q → ¬R)∧¬P ∧R est la conjonction des trois formules : P ∧Q → ¬R, ¬P et R. Donc (P ∧Q → ¬R)∧¬P ∧R est faux dès que l'une des trois formules est fausse.
- De même, quand P est vrai, ¬P est faux, ce qui entraîne que la conjonction (P ∧ Q → ¬R) ∧ ¬P ∧ R est également fausse et donc que la formule F est vraie.
On en déduit immédiatement la ligne (8).
- Il ne reste plus qu'à évaluer de manière classique la ligne (4) de la table de vérité.
| P | Q | R | P ∧ Q | ¬R | F1 | ¬P | F2 | F1 ∧ F2 | ¬Q | F | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F | F | F | . . . . . | . . . | . . | . . . | . . | . . . . . | . . . | T | (1) | |
| F | F | T | . . . . . | . . . | . . | . . . | . . | . . . . . | . . . | T | (2) | |
| F | T | F | . . . . . | . . . | . . | . . . | . . | . . . . . | . . . | T | (3) | |
| F | T | T | F | F | T | T | T | T | F | F | (4) | |
| T | F | F | . . . . . | . . . | . . | . . . | . . | . . . . . | . . . | T | (5) | |
| T | F | T | . . . . . | . . . | . . | . . . | . . | . . . . . | . . . | T | (6) | |
| T | T | F | . . . . . | . . . | . . | . . . | . . | . . . . . | . . . | T | (7) | |
| T | T | T | . . . . . | . . . | . . | . . . | . . | . . . . . | . . . | T | (8) |
Traduction
Traduire en formule logique les énoncés suivants, puis étudier leur validité et leur consistance :
- Quand on fait de l'alpinisme, on est montagnard ou sportif ;
un montagnard est un sportif ;
donc, quand on n'est pas sportif, on ne fait pas d'alpinisme. - Il ne dit rien s'il travaille ou s'il est seul ;
il se repose, mais il se tait ;
donc il est seul. - Jean ne sort que s'il fait beau ;
or, il pleut ;
donc, Jean reste chez lui. - Propositions élémentaires :
A ≡ Faire de l'alpinisme ;
M ≡ Être montagnard ;
S ≡ Être sportif.
Hypothèse 1 : H1 ≡ A → M ∨ S
Hypothèse 2 : H2 ≡ M → S
Conclusion : C ≡ ¬S → ¬A
Formulation : H1 ∧ H2 → C ≡ (A → M ∨ S) ∧ (M → S) → (¬S → ¬A)
Une table de vérité permettra de montrer que cette formule est valide (et donc, à fortiori, consistante). - Propositions élémentaires :
P ≡ Ne pas parler ;
T ≡ Travailler ;
S ≡ Être seul.
Hypothèse 1 : H ≡ T ∨ S → P
Hypothèse 2 : H ≡ ¬T ∧ P
Conclusion : C ≡ S
Formulation : H ∧ H → C ≡ (T ∨ S → P) ∧ (¬T ∧ P) → S
Une table de vérité permettra de montrer que cette formule est invalide, mais consistante. En fait, elle n'est fausse que dans l'interprétation :{m(T) = F, m(S) = F, m(P) = T}
- Propositions élémentaires :
S ≡ Sortir ;
B ≡ Beau temps.
Hypothèse 1 : H1 ≡ S → B
Hypothèse 2 : H2 ≡ ¬B
Conclusion : C ≡ ¬S
Formulation : H1 ∧ H2 → C ≡ (S → B) ∧ ¬B → ¬S
Une table de vérité permettra de montrer que cette formule est valide (et donc, à fortiori, consistante).
Démonstration
Montrer que les deux premières équivalences de l'absorption sont justes en utilisant, entre autres, la distributivité.
- A ∨ (¬A ∧ B) ≡ A ∨ B
≡ (A ∨ ¬A) ∧ (A ∨ B)
≡ T ∧ (A ∨ B)
≡ A ∨ B - A ∧ (¬A ∨ B) ≡ A ∧ B
≡ (A ∧ ¬A) ∨ (A ∧ B)
≡ F ∨ (A ∧ B)
≡ A ∧ B
Simplification
En utilisant des équivalences de formules (propriété 1.1), tenter de trouver une forme plus simple pour les formules qui suivent. Entre parenthèses est précisée la règle d'équivalence utilisée pour la nouvelle formule. La règle de commutativité, qui intervient souvent, est généralement non spécifiée.
| 1. | (a → a) ∨ (a → b) | |
| ≡ (¬a ∨ a) ∨ (¬a ∨ b) | (1re de implication) | |
| ≡ T ∨ (¬a ∨ b) | (1re de complémentarité) | |
| ≡ T | (3e de élément neutre) |
| 2. | a ∧ (¬a ∨ c) | |
| ≡ a ∧ c | (2e de absorption) |
| 3. | ¬a ∧ (a → b) | |
| ≡ ¬a ∧ (¬a ∨ b) | (1re de implication) | |
| ≡ ¬a | (4e de absorption) |
| 4. | a ∨ (¬c ∨ (b → c)) | |
| ≡ a ∨ (¬c ∨ (¬b ∨ c)) | (1re de implication) | |
| ≡ ¬c ∨ c ∨ a ∨ ¬b | (1re de associativité) | |
| ≡ T ∨ a ∨ ¬b | (1re de complémentarité) | |
| ≡ T | (3e de élément neutre) |
| 5. | a ∧ ¬b ∨ b ∧ ¬a → a | |
| ≡ ¬((a ∧ ¬b) ∨ (b ∧ ¬a)) ∨ a | (1re de implication) | |
| ≡ (¬(a ∧ ¬b) ∧ ¬(b ∧ ¬a)) ∨ a | (1re de Morgan) | |
| ≡ ((¬a ∨ b) ∧ (¬b ∨ a)) ∨ a | (2e de Morgan) | |
| ≡ (¬a ∨ b ∨ a) ∧ (¬b ∨ a ∨ a) | (1re de distributivité) | |
| ≡ ( T ∨ b) ∧ (¬b ∨ a) | (1re de complémentarité et 2e de idempotence) | |
| ≡ T ∧ (¬b ∨ a) | (3e de élément neutre) | |
| ≡ ¬b ∨ a | (2e de élément neutre) |
4-3. Travaux dirigés 1.4.2▲
Algorithme de Quine
Étudiez la validité et la consistance de la formule suivante :
F = (P ∧ Q → ¬R) ∧ ¬P ∧ R → ¬Q
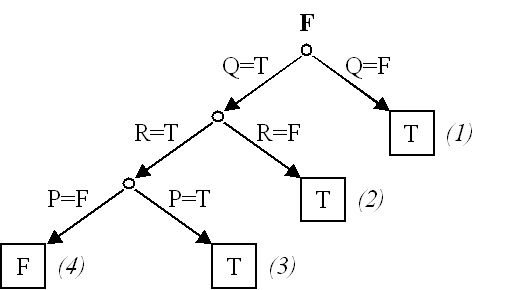
Cet algorithme permet de construire l'arbre sémantique partiel représenté sur la figure A.1. L'explication de la construction est la même que celle de la table de vérité partielle vue dans le TD 1.3.5Travaux dirigés (validité, consistance, formules équivalentes) pour cette même formule. La valeur (1) correspond à l'interprétation partielle {Q = F}. La formule F est donc vraie pour toutes les interprétations où Q est faux…
Algorithme de réduction
En utilisant l'algorithme de réduction, étudiez la validité de la formule suivante :
F = (A → B) ∧ (B → C) → (A → C)
On va suppose qu'il existe une assignation de A, B et C qui rend cette formule fausse.
On en déduit alors :
- (A → B)∧(B → C) est assigné à T et A → C est assigné à F (seule interprétation qui peut rendre la formule fausse) ;
- A → C assigné à F implique A = T et C = F ;
- (A → B) ∧ (B → C) assigné à T implique A → B assigné à T et B → C assigné à T ;
- A → B assigné à T implique A = F ou B = T, or, d'après (2), A = T, donc on ne peut avoir que B = T ;
- B → C assigné à T implique B = F ou C = T, or B = F est en contradiction avec (4) et C = T est en contradiction avec (2), donc la formule est valide.
4-4. Travaux dirigés 1.4.4▲
Formes conjonctives normales
Les formules suivantes sont-elles en forme conjonctive normale ? Combien contiennent-elles de clauses ?
| 1 | Oui, 0 | |
| 2 | Ø | oui, 1 |
| 3 | a ∨ b | oui, 1 |
| 4 | ¬(a ∨ b) ∨ c | non |
| 5 | a ∧ b ∧ ¬c | oui, 3 |
| 6 | a ∨ b ∧ c ∨ d | non |
| 7 | (a ∨ b) ∧ (¬a ∨ c) ∨ d | non |
| 8 | (a ∨ b) ∧ (¬a ∨ c ∨ d) | oui, 2 |
| 9 | (a ∨ b) ∧ (¬a ∨ c ∧ d) | non |
| 10 | (a ∨ b) ∧ (¬a ∨ c) ∧ d | oui, 3 |
| 11 | (¬a ∨ b) ∧ ¬(¬a ∨ c) ∧ (d ∨ e) | non |
| 12 | (¬a ∨ b) ∧ a ∧ ¬c ∧ (d ∨ e) | oui, 4 |
Normalisation
Forme normale conjonctive des formules :
- p ∧ q → p ∨ q,
f.n.c. : ¬p ∨ ¬q ∨ p ∨ q ;
f.n.c.p. sous d'ensemble de clauses : {} ; - p ∨ q → p ∧ q ,
f.n.c. : (¬p ∨ q) ∧ (¬q ∨ p) ;
f.n.c.p. sous d'ensemble de clauses : {¬p ∨ q , ¬q ∨ p} ; - p ↔ (p → r),
f.n.c. : (¬p ∨ r) ∧ p ;
f.n.c.p. sous d'ensemble de clauses : {¬p ∨ r} ; - p ↔ (q → r),
f.n.c. : (¬p ∨ ¬q ∨ r) ∧ (q ∨ p) ∧ (¬r ∨ p) ;
f.n.c.p. sous d'ensemble de clauses : {¬p ∨ ¬q ∨ r , q ∨ p , ¬r ∨ p} ;
4-5. Travaux dirigés 1.4.6▲
Principe de résolution
Voici le raisonnement que nous suivrons pour chacun des énoncés :
- F est valide ;
- ssi ¬F est inconsistant ;
- ssi l'ensemble de clauses correspondant à la forme conjonctive normale de ¬F est insatisfiable ;
- ssi on peut déduire Ø de cet ensemble de clauses.
- F ≡ (A → B) ∧ A → B
¬F ≡ (A → B) ∧ A ∧ ¬B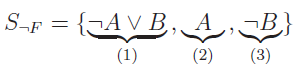
(a) Résolvante entre (3) et (1) : R4 = ¬A.
(b) Résolvante entre R4 et (2) : R5 = Ø.
F est valide. - F ≡ (A → B) ∧ ¬B → ¬A
¬F ≡ (A → B) ∧ ¬B ∧ A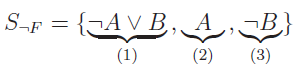
Même résolution que pour la formule 1. ci-dessus. - F ≡ (A → B) ∧ (B → C) → (A → C)
Non corrigé. - (A → M ∨ S) ∧ (M → S) → (¬S → ¬A)
Non corrigé.
Comparatif
Soit la formule suivante :
(p → q) ∧ ((q ∧ ¬r) → s) ∧ (¬t → (¬r ∧ ¬s)) → (p → t)
Table de vérité : la formule contient 5 variables propositionnelles différentes (p, q, r, s, et t), la table de vérité contiendra donc 2n = 32 lignes. Sa réalisation est relativement fastidieuse et le risque d'erreur sur une telle table n'est pas négligeable.
Non corrigé.
Table de vérité partielle Non corrigé.
Algorithme de Quine Non corrigé.
Principe de résolution Non corrigé.
Exercice complet
Traduire l'énoncé suivant dans le formalisme de la logique des propositions, puis étudier sa validité au moyen de l'algorithme de Quine puis du principe de résolution :
- quand un bateau fait naufrage, cela fait parler les journalistes ;
- les sponsors sont inquiets quand les journalistes parlent et qu'un bateau fait naufrage ;
- un bateau fait naufrage ;
- donc les sponsors sont inquiets.
Traduction de l'énoncé Non corrigé.
Algorithme de Quine Non corrigé.
Algorithme de réduction Non corrigé.
4-6. Travaux dirigés 1.4.8▲
Principe de résolution sur des clauses de Horn
Utiliser le principe de résolution appliqué à des clauses de Horn pour étudier la validité des énoncés suivants :
- (A → B) ∧ A → B
- (A → B) ∧ ¬B → ¬A
- (A → B) ∧ (B → C) → (A → C)
Enquête logique
Trois personnes, Adrien, Béatrice et Christophe, accusées d'un meurtre, déclarent respectivement :
- Béatrice est coupable et Christophe est innocent (Adrien) ;
- si Adrien est coupable, alors Christophe l'est aussi (Béatrice) :
- je suis innocent, mais au moins l'une des deux personnes est coupable (Christophe).
Utiliser le formalisme du calcul des propositions pour traduire les questions suivantes et donner la réponse :
- Les trois déclarations sont-elles compatibles ? (Non corrigé)
- L'un des témoignages peut-il se déduire des autres ? Lequel ? (Non corrigé)
- Si tous sont innocents, lequel a menti ? (Non corrigé)
- Si tous disent la vérité, qui est coupable ? (Non corrigé)
- Si seuls les innocents disent la vérité, qui est coupable ? (Non corrigé)


