1. Chapitre 1 - Logique des propositions▲
1-1. Introduction▲
Le but initial de la logique est de formaliser certaines relations qui peuvent apparaître de bon sens. Si je dis la phrase p : « il fait beau et je suis en vacances », cette phrase sera vraie si les deux propositions q : « il fait beau » et r : « je suis en vacances » sont vraies toutes les deux. Si l'une des deux est fausse, alors la phrase p sera fausse. Nous utilisons donc une interprétation intuitive du connecteur et qui nous permet de déterminer la valeur de vérité d'une phrase contenant deux sous-propositions reliées par et si nous connaissons la valeur de vérité de chacune des propositions. De même, nous utilisons un mécanisme semblable pour des phrases contenant les connecteurs ou, donc… c'est le principe de compositionnalité.
Logique des propositions
Le but du calcul propositionnel est de donner un fondement formel à un ensemble restreint d'énoncés du langage. Nous utiliserons comme éléments de base des propositions élémentaires (i.e. des énoncés déclaratifs) : « il fait beau », « je suis en vacances », etc.
Ces propositions élémentaires seront soit vraies, soit fausses (principe du tiers exclu). Pour former des phrases, à partir de ces propositions élémentaires, nous n'utiliserons que quatre connecteurs, et, ou, donc, équivalent à, ainsi que la négation (si la phrase « il fait beau » est vraie, alors « il ne fait pas beau » est fausse).
Pas de convention : divergence des interprétations
Plaçons-nous dans le contexte suivant : « Il aime les fraises et la chantilly ».
Dites si les propositions suivantes sont vraies ou fausses.
- « Il aime les fraises et il aime la chantilly ».
- « Il aime les fraises et il n'aime pas la chantilly ».
- « Il aime les fraises ou il aime la chantilly ».
- « Il aime les fraises ou il n'aime pas la chantilly ».
- « Il aime les fraises donc il aime la chantilly ».
- « Il aime les fraises donc il n'aime pas la chantilly ».
- « Il n'aime pas les fraises donc il aime la chantilly ».
- « Il n'aime pas les fraises donc il n'aime pas la chantilly ».
Il est probable que beaucoup ne seront pas d'accord sur toutes les réponses.
Convention d'interprétation des connecteurs
| P1 | P2 | P1 équivalent à P2 | P1 donc P2 | P1 et P2 | P1 ou P2 | |
|---|---|---|---|---|---|---|
| vrai | vrai | vrai | vrai | vrai | vrai | |
| vrai | faux | faux | faux | faux | vrai | |
| faux | vrai | faux | vrai | faux | vrai | |
| faux | faux | vrai | vrai | faux | faux |
| Proposition | non-Proposition |
|---|---|
| vrai | faux |
| faux | vrai |
Les conventions d'interprétation des connecteurs dyadiques(1), introduits dans la première section de l'introduction, sont définies par le tableau 1.1. On peut lire, par exemple, que (P1 équivalent à P2) est vrai lorsque P1 et P2 prennent les mêmes valeurs. Naturellement, nous interpréterons la négation comme indiqué dans le tableau 1.2.
Une interprétation qui a posé de nombreux problèmes est l'interprétation de l'implication (donc), et plus particulièrement des lignes 3 et 4, qui nous dit que si P1 est faux alors (P1 donc P2) est vrai quel que soit P2.
L'acception courante du terme voudrait probablement « si P1 alors P2 » soit vrai lorsque P1 et P2 sont vrais tous les deux et soit faux lorsque P1 est faux. La valeur vrai sur les lignes 3 et 4 de (P1 donc P2) deviendrait faux. Mais alors nous remarquons que donc est devenu synonyme de et. Ce n'est donc pas de cette manière-là qu'il nous faut résoudre ce « paradoxe » dit paradoxe de l'implication matérielle.
Il faut cependant remarquer que dans bien des situations, l'acception de « si… alors… » dans le langage courant recouvre bien la définition que nous donnons ici. Par exemple, soit la proposition « s'il fait beau, j'irai me promener ». S'il fait effectivement beau, j'irai me promener et ma proposition sera vraie. Par contre, s'il pleut, que j'aille ou que je n'aille pas me promener ne rend pas la proposition fausse. L'implication matérielle est donc bien reliée à une notion intuitive réelle.
Convention : convergence des interprétations
Nous avons dit que le but de la logique était de calculer des conclusions sûres. Une convention d'interprétation de nos quatre connecteurs et de notre négation vient d'être définie. Il nous reste maintenant à vérifier que ces conventions nous permettent de faire converger les réponses de l'exercice précédent.
Plaçons-nous dans le contexte suivant : « Il aime les fraises et la chantilly ».
Dites si les propositions suivantes sont vraies ou fausses.
- « Il aime les fraises et il aime la chantilly ».
- « Il aime les fraises et il n'aime pas la chantilly ».
- « Il aime les fraises ou il aime la chantilly ».
- « Il aime les fraises ou il n'aime pas la chantilly ».
- « Il aime les fraises donc il aime la chantilly ».
- « Il aime les fraises donc il n'aime pas la chantilly ».
- « Il n'aime pas les fraises donc il aime la chantilly ».
- « Il n'aime pas les fraises donc il n'aime pas la chantilly ».
Maintenant, tout le monde devrait être d'accord sur chacune des réponses.
1-2. Langage de la logique des propositions : (ie. syntaxe)▲
1-2-1. Définitions▲
Définition 1.1 -Alphabet- L'Alphabet de la logique des propositions (langage que l'on notera L) est constitué des symboles suivants :
- les formules { A, B, C… , φ, ψ… , p, q, r, s, t… },
- les connecteurs { ↔, →, ∧, ∨, ¬ },
- les délimiteurs { (,) }
Définition 1.2 -Atomes- Nous appellerons atomes ou variables propositionnelles ou propositions élémentaires des énoncés dont nous ne connaissons pas (et ne chercherons pas à connaître) la structure interne, et qui gardent leur identité tout au long du calcul propositionnel qui nous occupe.
L'ensemble des variables propositionnelles est noté v(L).
On désigne généralement des propositions élémentaires par des lettres minuscules de l'alphabet (habituellement p, q, r…).
Définition 1.3 -Connecteurs- Nous appellerons connecteurs propositionnels les symboles suivants :
- équivalence ↔;
- implication →;
- conjonction ∧;
- disjonction ∨;
- négation ¬.
Définition 1.4 -Formules- Nous dénoterons les formules (ou formules bien formées : fbf) par des lettres majuscules de l'alphabet latin ou grec (A, B… ou φ, ψ). L'ensemble des formules, noté F(L), est défini par :
- les atomes sont des formules (v(L) ⊆ F(L)) ;
- si φ et sont des formules, alors (φ ↔ ψ), (φ → ψ), (φ ∧ ψ), (φ ∨ ψ) et (¬φ) sont des formules.
Toute formule est obtenue par l'application des règles précédentes un nombre fini de fois.
L'ensemble des formules F(L) est infini, même si l'ensemble des propositions élémentaires v(L) est fini.
En appliquant strictement la définition ci-dessus de « Formules », nous dirions que p ↔ q → r n'est pas une formule bien formée. En effet, le parenthèsage est absent. On ne sait pas s'il s'agit de la formule ((p ↔ q) → r) ou s'il s'agit de (p ↔ (q → r)). Les parenthèses sont un moyen de lever l'ambiguïté. Il en existe un autre qui consiste à donner à chaque opérateur un ordre de priorité. Les connecteurs sont traditionnellement classés de la façon suivante (par priorité décroissante des connecteurs) : ¬, ∧, ∨, →, ↔. Dans le cas où deux connecteurs ont même priorité, et en l'absence de parenthèses, l'associativité se fait de gauche à droite. On peut ainsi se permettre d'omettre les parenthèses. Par exemple, la formule p → q ↔ ¬r doit se lire ((p → q) ↔ (¬r)). À l'avenir, lorsque nous parlerons de formules bien formées, nous inclurons également les formules dont le parenthèsage est partiellement ou complètement implicite. L'ensemble des formules bien formées ainsi défini forme le langage de la logique propositionnelle.
Définition 1.5 -Littéral- Un littéral est un atome (littéral positif) ou la négation d'un atome (littéral négatif).
Définition 1.6 -Clause- Une clause est une disjonction de littéraux (p1 ∨ p2 ∨… ∨ pn), les littéraux pouvant être positifs ou négatifs.
1-2-2. Travaux dirigés (la syntaxe)▲
Formules bien formées
Les « formules » suivantes sont-elles des formules bien formées ?
- a ∨ b ∧ c
- ¬a ∨ b ∧ c
- a ∨ ¬b ∧ c
- a¬ ∨ b ∧ c
- (a)
- (a)b
- ¬b(a)
- a ∨ ¬(b ∧ c)
- a¬(∨b ∧ c)
- a → b
- a ← a
- a → b ↔ c
- a → ¬(b ↔ c)
- a¬ → b
- a ∨ (b ↔ c)¬c → d
- a ∨ (b ↔ c) → ¬c → d
Parenthèsage
Explicitez le parenthèsage implicite des formules suivantes :
- a → b → c
- a ∨ b ∧ c
- a ∨ b ∧ c ↔ d → ¬ e ∨ f ∧ g
Simplifiez au maximum le parenthèsage des formules suivantes :
- (a)
- ((a ∨ b))
- ((a) ∧ (b))
- (¬(a ∨ b))
- ¬(((a) ∧ b))
- a ∨ (b ∧ c)
- (a ∨ b) ∧ c
- ((a ∧ b) → c)
- (a ∧ (b → c))
- ((a ∨ b) ∧ c) ↔ e
- (((a ∨ b) ∧ c) ↔ e) → f
- ((a ∧ b) ∨ c) ↔ (e → f)
- (((a → b) → c) → d)
- (a ∧ (b ∧ c))
- (a → (b → c))
Formalisation d'un énoncé (premier pas vers la sémantique)
Traduisez les énoncés suivants en formule logique :
- Quand il fait beau, Jean est heureux ;
il fait soleil ;
donc, Jean est heureux. - Quand il fait beau, Jean est heureux ;
or, il fait mauvais ;
donc Jean est malheureux. - Quand il fait beau, Jean est heureux ;
or, Jean est malheureux ;
donc il fait mauvais.
La qualité et la correction de la traduction ne sont pas du ressort de la logique.
1-3. Théorie des modèles (ie. sémantique)▲
1-3-1. Introduction▲
La théorie des modèles a pour but d'établir un mécanisme sémantique d'évaluation des formules. Par sémantique, nous entendons que nous allons donner un sens à nos atomes, puis donner un sens à une formule à partir de la valeur de vérité des atomes qui la composent et des connecteurs qui relient ces atomes. La théorie des modèles est une formalisation de la notion intuitive que nous avons de la vérité ou de la fausseté d'une phrase en fonction des propositions qui la composent.
En calcul propositionnel, ce résultat est obtenu en donnant à chaque atome une valeur de vérité et en associant à chaque connecteur une table de vérité qui, en fonction de la valeur de vérité des arguments du connecteur, donne la valeur de vérité de la formule constituée (nous avons déjà introduit de telles tables, cf. section 1.1Introduction).
Notre hypothèse(2), en calcul propositionnel, est donc que chaque atome ne peut prendre que deux valeurs : vrai (T) ou faux (F), et que la valeur de vérité d'une composition de formules est entièrement déterminée par la valeur de chacun de ses arguments.
1-3-2. Définitions▲
Définition 1.7 -Valuation- On appelle valuation, ou L-Modèle, d'un ensemble de variables propositionnelles v ⊆ v(L), une fonction m de v(L) dans { T,F} (i.e. m : v(L) → { T,F}).
L'ensemble des valuations (L-modèles) est noté M(L), ou plus simplement ML.
Définition 1.8 -Sémantique des connecteurs- Soit A et B deux formules, la sémantique des connecteurs est donnée par les tables de vérité représentées dans les tableaux 1.3 et 1.4.
| A | B | A ↔ B | A → B | A ∧ B | A ∨ B | |
|---|---|---|---|---|---|---|
| T | T | T | T | T | T | |
| T | F | F | F | F | T | |
| F | T | F | T | F | T | |
| F | F | T | T | F | F |
| A | ¬A |
|---|---|
| T | F |
| F | T |
Définition 1.9 -Interprétation d'une formule- Une interprétation d'une formule dans laquelle apparaissent les variables propositionnelles v1… ,vn est une valuation de {v1… ,vn}.
Une formule composée de n atomes propositionnels admet 2n interprétations.
Exemple : soit la formule F = (a ∧ b) ∨ ¬b → ¬a, {m(a) = T, m(b) = F} est une interprétation de F.
Définition 1.10 -Modèle d'une formule- Une interprétation I est un modèle d'une formule φ si elle est vraie (si elle vaut T).
1-3-3. Validité et consistance▲
Définition 1.11 -Formule valide- Une formule valide, ou tautologie, est une formule φ vraie quelles que soient les valeurs de vérité des atomes qui la composent (i.e. Vraie dans toute interprétation). On la note |= φ.
Définition 1.12 -Formule insatisfiable- Une formule insatisfiable, ou sémantiquement inconsistante, ou encore antitautologie, est une formule fausse dans toute interprétation.
Définition 1.13 -Formules satisfiables- Une formule satisfiable ou sémantiquement consistante est une formule vraie dans au moins une interprétation.
Définition 1.14 -Formules invalides- Une formule invalide est fausse dans au moins une interprétation.
Définition 1.15 -Formules contingentes- Une formule contingente est vraie dans certaines interprétations et fausse dans d'autres.
Définition 1.16 -Conséquence valide- Soit deux formules A et B. Nous dirons que A est la conséquence valide de B (A |= B) si tout modèle de A est un modèle de B.
Remarques
Soit une formule bien formée A, on a :
- A valide entraîne A consistante ;
- A inconsistante entraîne A invalide ;
- A est valide si et seulement si ¬A est inconsistante.
Trois cas se présentent pour A:
- soit A est valide (donc consistante) ;
- soit A est invalide, mais consistante (i.e. contingente) ;
- soit A est inconsistante (donc invalide).
1-3-4. Équivalence des formules bien formées▲
Définition 1.17 -Formules équivalentes- Deux formules sont équivalentes quand elles ont même valeur dans toute interprétation (notation : A ≡ B).
Théorème 1.1 -Règle de substitution uniforme- Soit la formule φ contenant les atomes p1, p2… ,pn. Soit la formule φ∗ obtenue en substituant aux atomes p1,p2… ,pn les formules ψ1, ψ2… , ψn. Alors si |= φ, on a |= φ∗.
Propriété 1.1 -Formules équivalentes- Soit A, B et C trois formules bien formées.
Implication
- A → B ≡ ¬A ∨ B
- ¬(A → B) ≡ A ∧ ¬B
- A ↔ B ≡ (A → B) ∧ (B → A)
Idempotence
- A ∧ A ≡ A
- A ∨ A ≡ A
Commutativité
- A ∨ B ≡ B ∨ A
- A ∧ B ≡ B ∧ A
Associativité
- (A ∨ B) ∨ C ≡ A ∨ (B ∨ C)
- (A ∧ B) ∧ C ≡ A ∧ (B ∧ C)
Distributivité
- A ∨ (B ∧ C) ≡ (A ∨ B) ∧ (A ∨ C)
- A ∧ (B ∨ C) ≡ (A ∧ B) ∨ (A ∧ C)
Élément neutre
- A ∨ F ≡ A
- A ∧ T ≡ A
- A ∨ T ≡ T
- A ∧ F ≡ F
Complémentarité
- A ∨ ¬A ≡ T
- A ∧ ¬A ≡ F
Involution
- ¬¬A ≡ A
De Morgan
- ¬(A ∨ B) ≡ ¬A ∧ ¬B
- ¬(A ∧ B) ≡ ¬A ∨ ¬B
Absorption
- A ∨ (¬A ∧ B) ≡ A ∨ B
- A ∧ (¬A ∨ B) ≡ A ∧ B
- A ∨ (A ∧ B) ≡ A
- A ∧ (A ∨ B) ≡ A
1-3-5. Travaux dirigés (validité, consistance, formules équivalentes)▲
Équivalence de formules
À l'aide d'une table de vérité, vérifiez les deux équivalences de Morgan.
Valeur de formules
- À l'aide d'une table de vérité, étudiez la validité et la consistance des formules que vous avez trouvées pour l'exercice « Formalisation d'un énoncé » du TD 1.2.2Travaux dirigés (la syntaxe).
- À l'aide d'une table de vérité, étudiez la validité et la consistance de la formule suivante : F = (P ∧ Q → ¬R) ∧ ¬P ∧ R → ¬Q
Traduction
Traduire en formule logique les énoncés suivants, puis étudier leur validité et leur consistance :
- Quand on fait de l'alpinisme, on est montagnard ou sportif ;
un montagnard est un sportif ;
donc, quand on n'est pas sportif, on ne fait pas d'alpinisme. - Il ne dit rien s'il travaille ou s'il est seul ;
il se repose, mais il se tait ;
donc il est seul. - Jean ne sort que s'il fait beau ;
or, il pleut ;
donc, Jean reste chez lui.
Démonstration
Montrer que les deux premières équivalences de l'absorption (A ∨ (¬A ∧ B) ≡ A ∨ B et A ∧ (¬A ∨ B) ≡ A ∧ B) sont justes en utilisant, entre autres, la distributivité.
Simplification
En utilisant des équivalences de formules, tenter de trouver une forme plus simple pour les formules suivantes :
- (a → a) ∨ (a → b)
- a ∧ (¬a ∨ c)
- ¬a ∧ (a → b)
- a ∨ (¬c ∨ (b → c))
- a ∧ ¬b ∨ b ∧ ¬a → a
1-3-6. Travaux pratiques : tables de vérité sous Excel▲
Introduction
Nous allons travailler avec le logiciel Microsoft Excel que vous devez déjà avoir manipulé (ce TP ne constitue pas une initiation aux manipulations de base sous Microsoft Excel).
Dans ce logiciel, T se notera VRAI et F se notera FAUX. ¬A s'écrira NON(A), A∨B s'écrira OU(A;B) et A ∧ B s'écrira ET(A;B). Toutes les formules doivent commencer par le signe « = ».
Bien entendu, les variables A et B doivent être remplacées par des coordonnées de cellule, par exemple ET(B3;C3) si les cellules B3 et C3 contiennent la valeur logique des variables A et B dont on cherche à évaluer la conjonction.
Tous les autres opérateurs n'existent pas et doivent être obtenus à l'aide des formules équivalentes constituées des trois opérateurs existants.
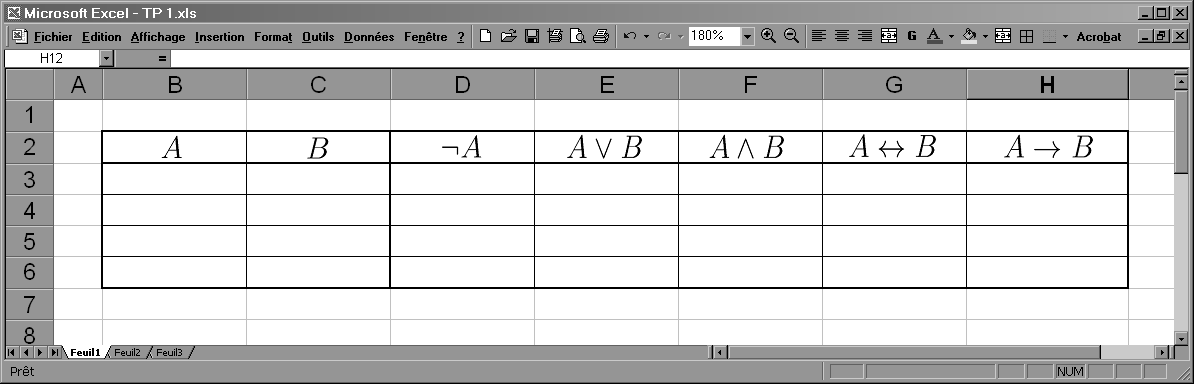
On se propose d'établir la table de vérité des 5 connecteurs logiques que nous avons vus à l'aide du logiciel Microsoft Excel. Voir la figure 1.1 pour une capture d'écran de la feuille de calcul correspondant au TP1.
- Remplir les colonnes B et C du tableau pour obtenir toutes les valuations possibles de l'ensemble de variables propositionnelles {A,B}.
- Saisir, dans les cellules de la ligne 3 du tableau, les formules correspondant à nos 5 connecteurs. Par exemple, dans la cellule D3 on saisira = NON(B3).
- Faire un copier-coller vers les trois lignes au-dessous.
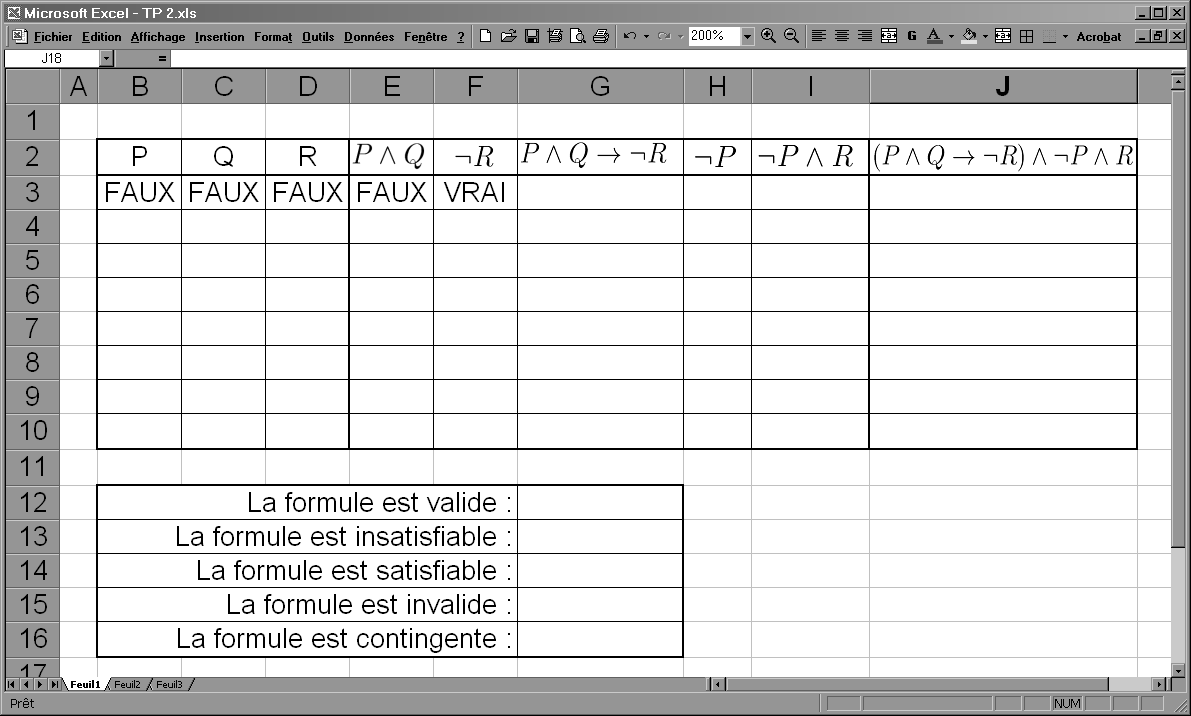
Travail pratique 2
On se propose d'établir la table de vérité de la formule F = (P ∧ Q → ¬R) ∧ ¬P ∧ R → ¬Q à l'aide du logiciel Microsoft Excel. Voir la figure 1.2 pour une capture d'écran de la feuille de calcul correspondant au TP2.
- Remplir les colonnes B et C et D du tableau pour obtenir toutes les valuations possibles de l'ensemble de variables propositionnelles {P,Q,R}. On ne rentrera manuellement que les valeurs de la première ligne. On cherchera ensuite un moyen pour systématiser et automatiser le remplissage des autres lignes.
- Écrire les formules et faire le copier/coller pour remplir le reste du tableau.
- Trouver les formules logiques qui permettent de remplir automatiquement les cellules G12 à G16.
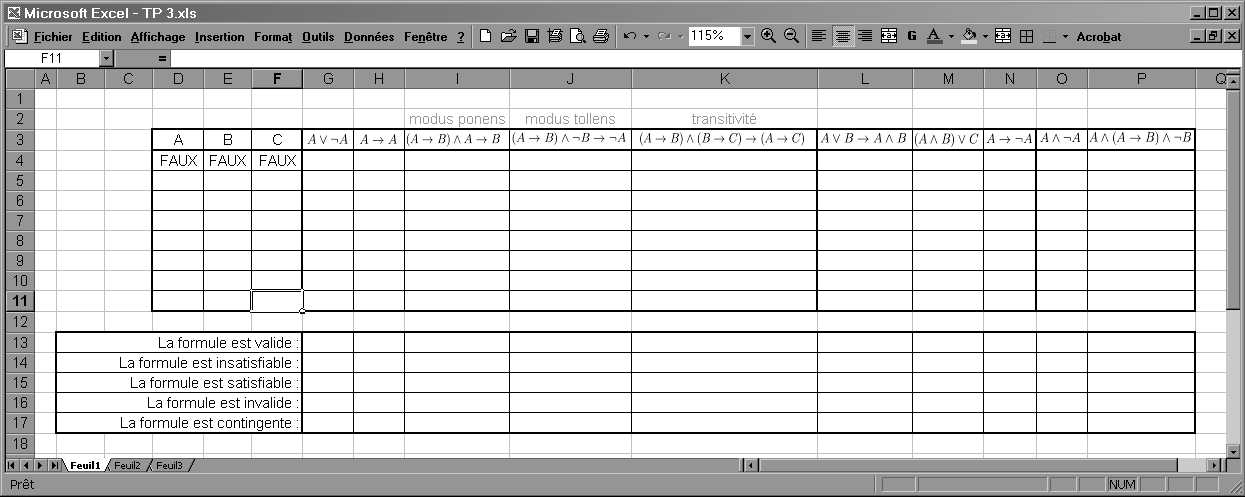
Travail pratique 3
On se propose d'étudier la validité et la consistance de différentes formules. Voir la figure 1.3 pour une capture d'écran de la feuille de calcul correspondant au TP3.
Le déroulement de ce TP est analogue à celui du TP2. Les colonnes intermédiaires pour faciliter l'évaluation des formules sont absentes, il faudra donc saisir des formules plus complexes dans le tableau.
1-4. Calcul propositionnel et résolution▲
Le but de ce chapitre est d'exposer des méthodes algorithmiques permettant de déterminer la satisfiabilité d'une formule, d'un ensemble de clauses et de faire de la démonstration automatique.
1-4-1. Principe de déduction▲
Introduction
Nous avons déjà vu une méthode générale pour établir la validité et la consistance d'une formule : la méthode des tables de vérité. Cependant, cette méthode réclame, pour une formule contenant n atomes distincts, le calcul d'une table comprenant 2n lignes. Il faut donc essayer de trouver des méthodes plus efficaces.
Le principe de déduction ramène toute preuve de déduction à une preuve d'inconsistance.
Cela nous permettra de nous concentrer uniquement sur les mécanismes de preuve d'inconsistance.
Il faut cependant signaler un résultat théorique important : le problème de satisfiabilité d'une formule propositionnelle quelconque est NP-complet. Cela signifie qu'il n'existe presque certainement aucun algorithme efficace permettant de calculer une affectation qui satisfait une formule, ou de vérifier sa validité.
Définitions
On a pu voir (définition 1.16) qu'une formule est insatisfiable si et seulement si elle n'a pas de modèle. Cette notion s'étend simplement à un ensemble de formules :
Définition 1.18 -Ensemble de formules insatisfiables- Un ensemble de formules est insatisfiable, ou (sémantiquement) inconsistant, si et seulement s'il n'existe aucune interprétation M telle que chaque formule A de E soit satisfaite par M.
Il découle de la définition précédente et de la notion de conséquence valide (définition 1.16) que :
Théorème 1.2 -Principe de déduction- Une formule A est la conséquence valide d'un ensemble de formules E ssi E ∪ {¬A} est insatisfiable.
En effet, toute interprétation est :
- soit c'est un modèle de E, et c'est alors un modèle de A, et donc certainement pas un modèle de E ∪ {¬A} ;
- soit ce n'est pas un modèle de E, et ce n'est donc pas, a fortiori, un modèle de E ∪ {A}.
Réciproquement, si E ∪ {¬A} est insatisfiable, cela implique que toute interprétation qui satisfait E ne satisfait pas ¬A, et satisfait donc A.
Les arbres sémantiques
Cette méthode n'est pas plus efficace que la méthode classique des tables de vérité. Elle consiste à construire pour une formule F contenant les atomes de S = {p1… ,pn}, un arbre binaire d'après les règles suivantes :
- chaque arc est étiqueté par un littéral p ou ¬p avec p ∈ S. La branche p correspond à une affectation de T à p alors que la branche ¬p correspond à l'affectation de F à p ;
- les littéraux étiquetant les deux arcs issus d'un même nœud sont opposés ;
- aucune branche ne comporte plus d'une occurrence de chaque atome.
Un arbre sémantique est dit complet si chaque branche contient une fois chaque atome.
Il est dit partiel dans le cas contraire. De la même manière que la table de vérité de F contient 2n lignes, un arbre sémantique complet comprend 2n feuilles.
Algorithme de Quine
L'Algorithme de Quine est une amélioration des arbres sémantiques. À chaque nœud de l'arbre binaire, on réalise une évaluation partielle en prenant en compte tous les atomes dont la valeur est déterminée. Si cette évaluation permet de conclure directement, on ne poursuit pas la construction à partir de ce nœud.
Algorithme de réduction
Basée sur un mécanisme de preuve par l'absurde, cette méthode peut être avantageusement utilisée quand la formule comprend de nombreuses implications. Elle consiste à supposer que la formule initiale est fausse, puis à en déduire les sous-valeurs logiques de chacune des deux sous-formules placées de chaque côté de l'implication et à réitérer le processus jusqu'au bout.
Voici un exemple. Soit la formule : ((p ∧ q) → r) → (p → (q → r)). On va supposer qu'il existe une assignation de p, q, r qui rend cette formule fausse. On en déduit alors :
- (p ∧ q) → r est assignée à T ;
- p → (q → r) est assignée à F.
À partir de ces éléments, on peut appliquer à nouveau le processus sur (2) ; on obtient alors que p est T, et enfin que q est T et r est F. Or cette affectation est en contradiction avec (1). Donc la formule est valide.
1-4-2. Travaux dirigés (algorithmes de Quine et de réduction)▲
Algorithme de Quine
En utilisant l'algorithme de Quine, étudiez la validité et la consistance de la formule suivante : F = (P ∧ Q → ¬R) ∧ ¬P ∧ R → ¬Q
Algorithme de réduction
En utilisant l'algorithme de réduction, étudiez la validité de la formule suivante : F = (A → B) ∧ (B → C) → (A → C)
1-4-3. Formes normales▲
Les méthodes précédentes (table de vérité, arbre sémantique, algorithme de Quine, algorithme de réduction) sont inefficaces dans la pratique. En exploitant une forme simplifiée d'expression de formules, certaines méthodes peuvent être plus efficaces en moyenne.
Définition 1.19 -Forme conjonctive normale- Une forme normale conjonctive est une conjonction de clauses.
La forme conjonctive normale d'une formule n'est pas unique.
On considère souvent une forme conjonctive normale C1 ∧ … ∧ Cn comme un ensemble de clauses et on la note alors : {C1… ,Cn}. On utilise ainsi souvent une terminologie ensembliste lorsque l'on parle de forme conjonctive normale (on dit, par exemple, qu'une clause appartient à une forme conjonctive normale).
Théorème 1.3 -Théorème de normalisation- Toute formule admet une forme conjonctive normale qui lui est logiquement équivalente.
Algorithme de normalisation - À partir d'une formule quelconque, voici comment construire la forme conjonctive normale associée.
- On remplace toutes les occurrences de (A ↔ B) par (A → B) ∧ (B → A). Ceci supprime toutes les occurrences du connecteur ↔.
- On remplace toutes les occurrences de (A → B) par (¬A∨B). Ceci supprime toutes les occurrences du connecteur →.
- On applique récursivement les règles de réécriture suivantes :
¬(A ∧ B) ; (¬A ∨ ¬B) ;
¬(A ∨ B) ; (¬A ∧ ¬B).
On ne trouve plus maintenant d'occurrence de ¬ que devant des atomes, ou devant d'autres occurrences de ¬. - On supprime toutes les doubles occurrences de la négation : ¬¬A ; A. Il ne reste alors plus que des occurrences uniques de ¬ placées directement devant les atomes.
- On applique la règle de distributivité : A ∨ (B ∧ C) ; (A ∨ B) ∧ (A ∨ C). (On peut également avoir à appliquer la commutativité de ∨ si l'expression est « dans le mauvais sens » ).
La formule obtenue est une forme normale équivalente à la formule de départ.
Une clause d'une forme normale contenant deux littéraux p et ¬p est valide et peut être supprimée de la forme normale sans que son sens soit modifié.
Définition 1.20 -Forme conjonctive normale pure- Une forme normale ne contenant aucune clause valide est dite forme conjonctive normale pure.
Remarques :
- si une clause Ci, élément d'une forme normale, contient une clause Cj , élément de la même forme normale, la clause Ci peut être supprimée de la forme normale sans que son sens ne soit changé ;
- une forme normale vide est valide ;
- une forme normale contenant la clause vide est inconsistante ;
- les formules valides ont une forme normale pure vide ; le test de validité d'une forme normale est trivial ;
- on réduit classiquement deux clauses opposées (A ∧ ¬A) en Ø, et n'importe quelle conjonction de clauses avec « ∧ », par exemple A ∧ Ø, à Ø. La clause Ø est la seule clause inconsistante.
1-4-4. Travaux dirigés (normalisation)▲
Formes conjonctives normales
Les formules suivantes sont-elles en forme conjonctive normale ? Combien contiennent-elles de clauses ?
- ;
- Ø ;
- a ∨ b ;
- ¬(a ∨ b) ∨ c ;
- a ∧ b ∧ ¬c ;
- a ∨ b ∧ c ∨ d ;
- (a ∨ b) ∧ (¬a ∨ c) ∨ d ;
- (a ∨ b) ∧ (¬a ∨ c ∨ d) ;
- (a ∨ b) ∧ (¬a ∨ c ∧ d) ;
- (a ∨ b) ∧ (¬a ∨ c) ∧ d ;
- (¬a ∨ b) ∧ ¬(¬a ∨ c) ∧ (d ∨ e) ;
- (¬a ∨ b) ∧ a ∧ ¬c ∧ (d ∨ e).
Normalisation
Trouver une forme normale conjonctive des formules suivantes :
- p ∧ q → p ∨ q ;
- p ∨ q → p ∧ q ;
- p ↔ (p → r) ;
- p ↔ (q → r).
1-4-5. Principe de résolution▲
Le principe de résolution est formé d'une unique règle d'inférence. Sa grande simplicité de mise en œuvre en fait une méthode très utilisée.
Nous avons vu qu'un ensemble de clauses est inconsistant si et seulement si Ø est une conséquence valide de cet ensemble. L'algorithme de résolution va construire des conséquences valides de notre ensemble N de départ jusqu'à obtention de la clause vide.
Théorème 1.4 -Principe de résolution- Soit N une forme normale, C1 et C2 deux clauses de N. Soit p un atome tel que p ∈ C1 et ¬p ∈ C2. Soit la clause R = C1 \{p}∪C2 \{¬p}. Alors les formes normales N et N ∪R sont logiquement équivalentes.
La clause R est appelée résolvante de C1 et C2.
Exemple :
- C1 = ¬M ∨ S, C2 = M ∨ S, la résolvante de C1 et C2 est R = S ;
- C1 = ¬M, C2 = P ∨M ∨ S, la résolvante de C1 et C2 est R = S ∨ P ;
- C1 = A ∨ B, C2 = ¬B ∨ C ∨ D, la résolvante de C1 et C2 est R = A ∨ C ∨ D ;
- C1 = A ∨ B, C2 = A ∨ C, il n'y a pas de résolvante ;
- C1 = ¬B∨A, C2 = B∨C∨¬A il y a deux résolvantes pour C1 et C2, R1 = A∨C∨¬A et R2 = ¬B ∨ B ∨ C ; ces deux résolvantes sont des tautologies et n'apportent rien.
Le principe de résolution peut s'avérer très efficace dès lors que l'on sait choisir les bonnes clauses dans le bon ordre, mais il ne fournit pas, en général, de méthode plus efficace que les algorithmes vus précédemment.
Application
Nous voulons démontrer que : {p → r, q → r} (p ∨ q) → r.
- D'après le théorème de déduction, l'énoncé précédent se ramène à : {p → r, q → r, ¬((p ∨ q) → r)} |= Ø.
- Il nous reste donc à démontrer que {p → r, q → r, ¬((p ∨ q) → r)} est inconsistant.
- En ramenant notre ensemble de clauses en forme normale, nous obtenons : {¬p ∨ r, ¬q ∨ r, p ∨ q, ¬r}.
- Nous allons appliquer le principe de résolution pour démontrer cette inconsistance.
Nous allons numéroter nos clauses
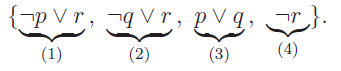
puis dérouler les conséquences valides.
- (5) ¬p à partir de 1 et 4.
- (6) ¬q à partir de 2 et 4.
- (7) q à partir de 5 et 3.
- Ø à partir de 6 et 7.
Le résultat a été obtenu de façon rapide principalement parce que l'on a su choisir les bonnes clauses dans le bon ordre.
Remarque
Comme nous l'avons déjà dit, le test de validité d'une forme normale est trivial puisque les formules valides ont une forme normale pure vide. Mais alors à quoi sert le principe de résolution ? En fait, le principe de résolution est surtout utile en logique des prédicats.
C'est la base du langage prolog. Le principe de résolution n'est pas vraiment utile en logique des propositions.
1-4-6. Travaux dirigés (principe de résolution I)▲
Principe de résolution
Utiliser le principe de résolution pour étudier la validité des énoncés suivants :
- (A → B) ∧ A → B
- (A → B) ∧ ¬B → ¬A
- (A → B) ∧ (B → C) → (A → C)
- (A → M ∨ S) ∧ (M → S) → (¬S → ¬A)
- (T ∨ S → P) ∧ (¬T ∧ P) → S
Comparatif
Soit la formule suivante : (p → q) ∧ ((q ∧ ¬r) → s) ∧ (¬t → (¬r ∧ ¬s)) → (p → t)
Étudier la validité de la formule par les moyens suivants :
- table de vérité partielle ;
- algorithme de Quine (arbre sémantique partiel) ;
- le principe de résolution.
Exercice complet
Traduire l'énoncé suivant dans le formalisme de la logique des propositions, puis étudier sa validité au moyen de l'algorithme de Quine puis du principe de résolution :
- quand un bateau fait naufrage, cela fait parler les journalistes ;
- les sponsors sont inquiets quand les journalistes parlent et qu'un bateau fait naufrage ;
- un bateau fait naufrage ;
- donc les sponsors sont inquiets.
1-4-7. Principe de résolution adapté aux clauses de Horn▲
La méthode de résolution est, dans le cas général, inefficace. Il existe cependant des cas particuliers où cette méthode est rapide.
Nous allons nous intéresser dans ce chapitre à un type particulier de forme normale, les formes normales composées de clause de Horn.
Définition 1.21 -Clause de Horn- Une clause de Horn est une clause comportant au plus un littéral positif. Il existe donc trois types de clauses de Horn :
- celles comportant un littéral positif et au moins un littéral négatif, appelées clauses de Horn strictes ;
- celles comportant un littéral positif et aucun littéral négatif, appelées clauses de Horn positives ;
- celles ne comportant que des littéraux négatifs, appelées clauses de Horn négatives (et dont fait partie la clause vide Ø).
Algorithme de résolution adapté aux clauses de Horn
L'algorithme présenté ci-dessous constitue une amélioration de l'algorithme de résolution appliqué à une forme normale N ne contenant que des clauses de Horn.
- si Ø est dans N, l'ensemble est inconsistant et la résolution est terminée ;
- sinon, choisir une clause C et une clause P telles que P soit une clause de Horn positive réduite à p et C une clause contenant ¬p ;
- calculer la résolvante R de P et C ;
- reprendre l'algorithme en remplaçant N par (N \ {C}) ∪ R.
Cet algorithme peut se terminer de deux façons :
- nous avons abouti à Ø et l'ensemble N est alors inconsistant ;
- il est impossible de poursuivre, car nous ne parvenons plus à trouver P et C vérifiant les conditions requises ; la formule est alors consistante et le modèle composé de chacune des clauses positives restantes (ou plus exactement le modèle composé de chacun des atomes de ces clauses), lorsque l'algorithme se termine, est un modèle de N (on appelle d'ailleurs ce modèle le modèle canonique de N).
Remarques
- Nous nous permettons ici de remplacer N par (N \ {C}) ∪R alors que l'algorithme général demande d'utiliser N ∪ R. Mais dans le cas présent, la clause C est une conséquence valide de R, et peut donc être omise (deuxième formule équivalente de l'absorption). Nous engendrons donc bien des conséquences valides de N.
- On remarque que la résolvante R de P et C n'est autre que C \ {¬p}. On supprime donc à chaque étape un atome dans une clause de N. On est donc certain que l'algorithme aboutit. En ce qui concerne la complexité, il existe un algorithme linéaire résolvant le problème de la satisfiabilité d'un ensemble de clauses de Horn.
Exemple de résolution
Nous allons utiliser cette méthode pour démontrer l'inconsistance de : {¬p ∨ r,¬r ∨ s,p,¬s}
- Par sélection de p et ¬p ∨ r, l'ensemble se réduit à : {r,¬r ∨ s,p,¬s}.
- Par sélection de r et ¬r ∨ s, nous obtenons : {r,s,p,¬s}.
- Enfin, par sélection de s et ¬s : {r,s,p,Ø}.
L'ensemble de clauses est bien inconsistant.
Interprétation
Quel est le cadre d'application des clauses de Horn ? Ou encore, que peut-on représenter avec des clauses de Horn ?
- Les clauses de Horn positives, par exemple p, sont appelées faits. Il s'agit en effet de l'énoncé de la vérité logique d'un atome.
- Les clauses de Horn strictes q ∨ ¬p1 ∨ … ∨ ¬pn sont équivalentes à {p1… ,pn} |= q et représentent des règles du type si … alors …. Elles permettent de déduire de nouveaux faits à partir de faits existants.
- les clauses négatives peuvent se comprendre comme des buts à atteindre. Considérons que nous souhaitions prouver {H1… ,Hn} |= (p ∧ q ∧ r). La partie (p ∧ q ∧ r) est le but de notre résolution. En appliquant une technique d'inconsistance nous sommes ramenés à {H1… ,Hn,(¬p ∨ ¬q ∨ ¬r)} |= Ø. La clause (¬p ∨ ¬q ∨ ¬r) est une clause de Horn négative qui modélise donc bien le but à atteindre.
1-4-8. Travaux dirigés (principe de résolution II)▲
Principe de résolution sur des clauses de Horn
Utiliser le principe de résolution appliqué à des clauses de Horn pour étudier la validité des énoncés suivants :
- (A → B) ∧ A → B
- (A → B) ∧ ¬B → ¬A
- (A → B) ∧ (B → C) → (A → C)
Enquête logique
Trois personnes, Adrien, Béatrice et Christophe, accusées d'un meurtre, déclarent respectivement :
- Béatrice est coupable et Christophe est innocent (Adrien) ;
- si Adrien est coupable, alors Christophe l'est aussi (Béatrice) ;
- je suis innocent, mais au moins l'une des deux personnes est coupable (Christophe).
Utiliser le formalisme du calcul des propositions pour traduire les questions suivantes et donner la réponse :
- Les trois déclarations sont-elles compatibles ?
- L'un des témoignages peut-il se déduire des autres ? Lequel ?
- Si tous sont innocents, lequel a menti ?
- Si tous disent la vérité, qui est coupable ?
- Si seuls les innocents disent la vérité, qui est coupable ?