3. Chapitre 3 - Bases de données relationnelles▲
3-1. Introduction au modèle relationnel▲
3-1-1. Présentation▲
Le modèle relationnel a déjà été introduit dans la section 1.1.2Modèle de base de données.
Dans ce modèle, les données sont représentées par des tables, sans préjuger de la façon dont les informations sont stockées dans la machine. Les tables constituent donc la structure logique(6) du modèle relationnel. Au niveau physique, le système est libre d'utiliser n'importe quelle technique de stockage (fichiers séquentiels, indexage, adressage dispersé, séries de pointeurs, compression…) dès lors qu'il est possible de relier ces structures à des tables au niveau logique. Les tables ne représentent donc qu'une abstraction de l'enregistrement physique des données en mémoire.
Le succès du modèle relationnel auprès des chercheurs, concepteurs et utilisateurs est dû à la puissance et à la simplicité de ses concepts. En outre, contrairement à certains autres modèles, il repose sur des bases théoriques solides, notamment la théorie des ensembles et la logique des prédicats du premier ordre.
Les objectifs du modèle relationnel sont :
- proposer des schémas de données faciles à utiliser ;
- améliorer l'indépendance logique et physique (cf. section 1.2.2Objectifs) ;
- mettre à la disposition des utilisateurs des langages de haut niveau ;
- optimiser les accès à la base de données ;
- améliorer l'intégrité et la confidentialité ;
- fournir une approche méthodologique dans la construction des schémas.
De façon informelle, on peut définir le modèle relationnel de la manière suivante :
- les données sont organisées sous forme de tables à deux dimensions, encore appelées relations, dont les lignes sont appelées n-uplet ou tuple en anglais ;
- les données sont manipulées par des opérateurs de l'algèbre relationnelle ;
- l'état cohérent de la base est défini par un ensemble de contraintes d'intégrité.
Au modèle relationnel est associée a la théorie de la normalisation des relations qui permet de se débarrasser des incohérences au moment de la conception d'une base de données relationnelle.
3-1-2. Éléments du modèle relationnel▲
Définition 1 -attribut- Un attribut est un identificateur (un nom) décrivant une information stockée dans une base.
Exemples d'attribut : l'âge d'une personne, le nom d'une personne, le numéro de sécurité sociale.
Définition 2 -Domaine- Le domaine d'un attribut est l'ensemble, fini ou infini, de ses valeurs possibles.
Par exemple, l'attribut numéro de sécurité sociale a pour domaine l'ensemble des combinaisons de quinze chiffres et nom a pour domaine l'ensemble des combinaisons de lettres (une combinaison comme cette dernière est généralement appelée chaîne de caractères ou, plus simplement, chaîne).
Définition 3 -relation- Une relation est un sous-ensemble du produit cartésien de n domaines d'attributs (n > 0).
Une relation est représentée sous la forme d'un tableau à deux dimensions dans lequel les n attributs correspondent aux titres des n colonnes.
Définition 4 -schéma de relation- Un schéma de relation précise le nom de la relation ainsi que la liste des attributs avec leurs domaines.
Le tableau 3.1 montre un exemple de relation et précise son schéma.
| N° Sécu | Nom | Prénom |
|---|---|---|
| 354338532195874 | Durand | Caroline |
| 345353545435811 | Dubois | Jacques |
| 173354684513546 | Dupont | Lisa |
| 973564213535435 | Dubois | Rose-Marie |
Définition 5 -degré- Le degré d'une relation est son nombre d'attributs.
Définition 6 -occurrence ou n-uplets ou tuples- Une occurrence, ou n-uplets, ou tuples, est un élément de l'ensemble figuré par une relation. Autrement dit, une occurrence est une ligne du tableau qui représente la relation.
Définition 7 -cardinalité- La cardinalité d'une relation est son nombre d'occurrences.
Définition 8 -clé candidate- Une clé candidate d'une relation est un ensemble minimal des attributs de la relation dont les valeurs identifient à coup sûr une occurrence.
La valeur d'une clé candidate est donc distincte pour tous les tuples de la relation. La notion de clé candidate est essentielle dans le modèle relationnel.
Règle 9 Toute relation a au moins une clé candidate et peut en avoir plusieurs.
Ainsi, il ne peut jamais y avoir deux tuples identiques au sein d'une relation. Les clés candidates d'une relation n'ont pas forcément le même nombre d'attributs. Une clé candidate peut être formée d'un attribut arbitraire, utilisé à cette seule fin.
Définition 10 -clé primaire- La clé primaire d'une relation est une de ses clés candidates. Pour signaler la clé primaire, ses attributs sont généralement soulignés.
Définition 11 -clé étrangère- Une clé étrangère dans une relation est formée d'un ou plusieurs attributs qui constituent une clé primaire dans une autre relation.
Définition 12 -schéma relationnel- Un schéma relationnel est constitué par l'ensemble des schémas de relation.
Définition 13 -base de données relationnelle- Une base de données relationnelle est constituée par l'ensemble des n-uplets des différentes relations du schéma relationnel.
3-1-3. Passage du modèle entités-associations au modèle relationnel▲
3-1-3-a. Règles de passage▲
Pour traduire un schéma du modèle entités-associations vers le modèle relationnel, on peut appliquer les règles suivantes :
- La normalisation devrait toujours être effectuée avant le passage au modèle relationnel (cf. section 2.4.4Normalisation des types entité et type association). Dans les faits, elle est parfois faite a posteriori (section 3.2Normalisation), ce qui impose toujours une surcharge de travail importante.
- Chaque type entité donne naissance à une relation. Chaque attribut de ce type entité devient un attribut de la relation. L'identifiant est conservé en tant que clé de la relation.
- Chaque type association dont aucune patte n'a pour cardinalité maximale 1 donne naissance à une relation. Chaque attribut de ce type association devient un attribut de la relation. L'identifiant, s'il est précisé, est conservé en tant que clé de la relation, sinon cette clé est formée par la concaténation des identifiants des types entité qui interviennent dans le type association.
- Un type association dont au moins une patte a une cardinalité maximale à 1 (ce type association devrait être binaire et n'a généralement pas d'attribut) ne devient pas une relation. Il décrit en effet une dépendance fonctionnelle (cf. section 3.2Normalisation). La relation correspondant au type entité dont la patte vers le type association a une cardinalité maximale valant 1, se voit simplement ajouter comme attribut (et donc comme clé étrangère) l'identifiant de l'autre type entité.
3-1-3-b. Cas particulier d'un type association du type 1 vers 1▲
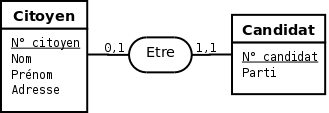
Dans l'exemple de la figure 3.1 toutes les cardinalités maximales du type association Etre sont de 1. L'application des règles de passage du modèle entités-associations au modèle relationnel énoncées ci-dessus nous donnerait :
- Citoyen(Num-Citoyen, Num-Candidat, Nom, Prénom, Adresse) ;
- Candidat(Num-Candidat), Num-Citoyen, Parti).
L'attribut Num-Candidat dans la relation Citoyen est une clé étrangère de la relation Candidat. L'attribut Num-Citoyen dans la relation Candidat est une clé étrangère de la relation Citoyen.
Le type association Etre étant du type 1 vers 1, il est entièrement matérialisé dans la relation Candidat par l'attribut Num-Citoyen. Il est donc inutile de la rematérialiser dans la relation Citoyen. L'attribut Num-Candidat dans la relation Citoyen doit donc être supprimé. D'autre part, dans la relation Candidat, l'attribut Num-Citoyen, en plus d'être une clé étrangère, constitue une clé candidate. On peut donc se passer de la clé Num-Candidat.
Le schéma relationnel adéquat correspondant au modèle entités-associations de la figure 3.1 devient donc :
- Citoyen(Num-Citoyen, Nom, Prénom, Adresse) ;
- Candidat(Num-Citoyen, Parti).
où Num-Citoyen, en plus d'être la clé de la relation Candidat, est une clé étrangère de la relation Citoyen.
3-1-3-c. Cas particulier d'un type entité sans attribut autre que sa clé▲
Lorsqu'un type entité ne possède pas d'attribut en dehors de sa clé, il ne faut pas nécessairement en faire une relation.
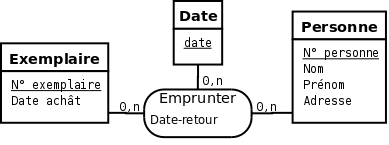
Par exemple, le type entité Date de la figure 3.2 ne doit pas se traduire par une relation. Le schéma relationnel adéquat correspondant au modèle entités-associations de la figure est donc :
- Exemplaire(Num-Exemplaire, date-achat) ;
- Personne(Num-Personne, nom, prénom, adresse) ;
- Emprunter(Num-Exemplaire, Num-Personne, Date, date-retour).
3-1-3-d. Exemple complet▲
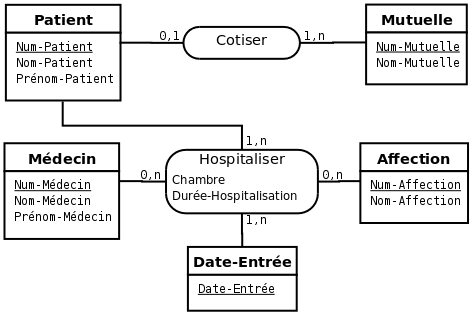
Comme exemple d'application, voici les relations déduites du schéma entités-associations de la figure 3.3 :
- Patient(Num-Patient, Nom-Patient, Num-Mutuelle) ;
- Mutuelle(Num-Mutuelle, Nom-Mutuelle) ;
- Médecin(Num-Médecin, Nom-Médecin, Prénom-Médecin) ;
- Affection(Num-Affection, Nom-Affection) ;
- Hospitaliser(Num-Patient, Num-Affection, Num-Médecin, Date-Entrée, Chambre, Durée-Hospitalisation).
3-2. Normalisation▲
3-2-1. Introduction▲
Les formes normales sont différents stades de qualité qui permettent d'éviter la redondance dans les bases de données relationnelles afin d'éviter ou de limiter : les pertes de données, les incohérences au sein des données, l'effondrement des performances des traitements.
Le processus de normalisation consiste à remplacer une relation donnée par certaines projections afin que la jointure de ces projections permette de retrouver la relation initiale. En d'autres termes, le processus est réversible (i.e. sans perte d'information). Les notions de projection et de jointure seront respectivement définies dans les sections 3.3.3Projection et 3.3.8Jointure, thêta-jointure, équijointure, jointure naturelle.
Il existe une hiérarchie dans les règles de normalisation : une relation en 5e forme normale est forcément en 4e forme normale, une relation en 4e forme normale est forcément en forme normale de Boyce-Codd, etc. Il existe des méthodes systématiques pour normaliser une relation dans chacune des formes normales. Ces algorithmes de décomposition, associés à chacune des formes normales, sortent du cadre de ce cours et ne seront pas abordés.
La normalisation peut être effectuée, et c'est préférable, pendant la phase de conception sur le modèle entités-associations (cf. section 2.4.4Normalisation des types entité et type association). Ce qui a été dit et les exemples qui ont été donnés dans cette section restent transposables au modèle relationnel. Dans le cas où la normalisation est faite en amont, lors de la conception, il n'est pas nécessaire de la recommencer sur le modèle relationnel. On peut tout de même vérifier que les relations obtenues par le passage du modèle entités-associations au modèle relationnel sont toujours en forme normale, mais, sauf erreur, il ne devrait pas y avoir de problème. Il en va tout autrement lorsque l'on ne connaît pas bien, ou maîtrise pas bien, l'origine d'un modèle relationnel. Dans ce cas, vérifier la normalisation des relations, et, le cas échéant, les normaliser, est une phase primordiale. C'est également le cas lorsque le modèle relationnel est le modèle de conception (i.e. on ne passe pas par un modèle entités-associations).
Contrairement à ce que nous avions fait dans la section 2.4.4Normalisation des types entité et type association dans le cadre du modèle entités-associations, nous abordons ici la normalisation en nous appuyant sur les notions de dépendance fonctionnelle, dépendance multivaluée et dépendance de jointure. Il est important de prendre conscience que la dépendance fonctionnelle, la dépendance multivaluée et la dépendance de jointure sont des notions sémantiques. Elles tirent leurs origines dans les contraintes du monde réel. Comme ces contraintes participent à la sémantique de la situation, elles doivent avoir une manifestation dans la base de données. Les dépendances doivent donc être spécifiées dans la définition de la base de données afin que le SGBD puisse les appliquer. Les concepts de normalisation fournissent en fait un moyen indirect de déclarer ces dépendances. Autrement dit, la normalisation d'une base de données est une manifestation observable des dépendances observées dans le monde réel. La dépendance fonctionnelle permet de définir les premières formes normales jusqu'à la forme normale de Boyce-Codd (1FN, 2FN, 3FN et BCNF). La dépendance multivaluée permet de définir la quatrième forme normale (4FN) et la dépendance de jointure la cinquième forme normale (5FN).
3-2-2. Dépendance fonctionnelle (DF)▲
Définition 14 -dépendance fonctionnelle (DF)- Soit R(A1, A2,… An) un schéma de relation, et X et Y des sous-ensembles de A1, A2,… An. On dit que X détermine Y ou que Y dépend fonctionnellement de X si, et seulement si, des valeurs identiques de X impliquent des valeurs identiques de Y. On le note : X → Y.
Autrement dit, il existe une dépendance fonctionnelle entre un ensemble d'attributs X et un ensemble d'attributs Y, que l'on note X → Y, si connaissant une occurrence de X on ne peut lui associer qu'une seule occurrence de Y.
Il est essentiel de noter qu'une dépendance fonctionnelle est une assertion sur toutes les valeurs possibles et non sur les valeurs actuelles : elle caractérise une intention et non une extension de la relation.
Définition 15 -dépendance fonctionnelle élémentaire- Une dépendance fonctionnelle élémentaire est une dépendance fonctionnelle de la forme X → A, où A est un attribut unique n'appartenant pas à X et où il n'existe pas X′ inclus au sens strict dans X (i.e. X′ ⊂ X) tel que X′ → A.
Autrement dit, une dépendance fonctionnelle est élémentaire si la cible est un attribut unique et si la source ne comporte pas d'attributs superflus. La question sur l'élémentarité d'une dépendance fonctionnelle ne doit donc se poser que lorsque la partie gauche de la dépendance fonctionnelle comporte plusieurs attributs.
Définition 16 -dépendance fonctionnelle directe- Une dépendance fonctionnelle X → A est une dépendance fonctionnelle directe s'il n'existe aucun attribut B tel que l'on puisse avoir X → B et B → A.
En d'autres termes, cela signifie que la dépendance entre X et A ne peut pas être obtenue par transitivité.
3-2-3. Première et deuxième forme normale▲
3-2-3-a. Première forme normale▲
Définition 17 -première forme normale (1FN)- Une relation est en première forme normale si, et seulement si, tout attribut contient une valeur atomique (non multiples, non composées).
Par exemple, le pseudo schéma de relation Personne(num-personne, nom, prénom, rue-et-ville, prénoms-enfants) n'est pas en première forme normale. Il faut le décomposer en :
- Personne(num-personne, nom, prénom, rue, ville) ;
- Prénoms-enfants(num-personne, num-prénom) ;
- Prénoms(num-prénom, prénom).
3-2-3-b. Remarques sur la première forme normale▲
La première forme normale impose que chaque ligne d'une relation ait une seule valeur pour chaque colonne (i.e. attribut), ce qui est justement la définition d'une table. Donc, une table est nécessairement en première forme normale au sens du modèle relationnel.
Cependant, il faut noter que le modèle relationnel peut être étendu de manière à permettre des colonnes à valeur complexe. On parle alors de modèle relationnel étendu (NF2 pour Non First Normal Form en anglais).
3-2-3-c. Deuxième forme normale▲
Définition 18 -deuxième forme normale (2FN)- Une relation est en deuxième forme normale si, et seulement si, elle est en première forme normale et si toutes les dépendances fonctionnelles entre la clé et les autres attributs sont élémentaires.
Une relation peut être en deuxième forme normale par rapport à une de ses clés candidates et ne pas l'être par rapport à une autre. Une relation avec une clé primaire réduite à un seul attribut est, par définition, forcément en deuxième forme normale.
3-2-4. Troisième forme normale▲
Définition 19 -Troisième forme normale (3FN)- Une relation est en troisième forme normale si, et seulement si elle est en deuxième forme normale et tout attribut n'appartenant pas à la clé n'est pas en dépendance fonctionnelle directe avec un ensemble d'attributs non-clé.
Une relation peut être en troisième forme normale par rapport à une de ses clés candidates et ne pas l'être par rapport à une autre. Une relation en deuxième forme normale avec au plus un attribut qui n'appartient pas à la clé primaire est, par définition, forcément en troisième forme normale.
3-2-5. Forme normale de BOYCE-CODD▲
Définition 20 -forme normale de BOYCE-CODD (BCNF)- Une relation est en forme normale de Boyce-Codd (BCNF) si, et seulement si, les seules dépendances fonctionnelles élémentaires sont celles dans lesquelles une clé détermine un attribut non-clé.
Cette forme normale permet de renforcer certaines lacunes de la troisième forme normale. Dans la pratique, la plupart des problèmes de conception peuvent être résolus en appliquant les concepts de troisième forme normale et de forme normale de BOYCE-CODD. Les quatrième et cinquième formes normales traitent encore d'autres cas de redondance, mais qui ne sont pas expliqués par des dépendances fonctionnelles.
3-2-6. Quatrième et cinquième forme normale▲
3-2-6-a. Dépendance multivaluée (DM)▲
Définition 21 -dépendance multivaluée (DM)- Soit R(A1, A2,… An) un schéma de relation contenant n propriétés, soit X, Y et Z des sous-ensembles de A1, A2,… An et soit Xi, Yi et Zi des instances de ces sous-ensembles (i.e. une affectation de valeur à chacune des propriétés de ces sous-ensembles). Il existe une dépendance multivaluée (DM) entre les ensembles de propriétés X, Y lorsque :
| (X1, Y1, Z1) ∈ R et (X1, Y2, Z2) ∈ R ⇒ (X1, Y1, Z2) ∈ R et (X1, Y2, Z1) ∈ R |
On la note X ↠ Y, ce qui se lit X multidétermine Y.
Remarque : X ↠ Y ⇒ X ↠ Ai−(X ∪ Y).
Comme illustration, supposons une situation où un employé d'un garage est qualifié pour effectuer un certain type d'intervention sur certaines marques de voiture. Cette situation est modélisée par le schéma relationnel suivant :
- Employé(Nom-Employé)
- Intervention(Type-Intervetion)
- Constructeur(Marque)
- Intervenir(Nom-Employé, Type-Intervetion, Marque)
Supposons maintenant qu'un employé qui effectue un ensemble de types d'interventions pour un ensemble de marques de voiture est capable d'effectuer chacun de ces types d'interventions sur chacune de ces marques de voitures. Dans ce cas, il existe des dépendances multivaluées dans la relation Intervenir : Nom-Employé ↠ Type-Intervetion et Nom-Employé ↠ Marque.
3-2-6-b. Quatrième forme normale▲
Définition 22 -quatrième forme normale (4FN)- Une relation est en quatrième forme normale (4FN) si, et seulement si, elle est en forme normale de BOYCE-CODD et si elle ne possède pas de dépendance multivaluée ou si, X ↠ Y étant la dépendance multivaluée, il existe une propriété A telle que X → A.
| Nom-Employé | Type-Intervention | Marque |
|---|---|---|
| Tussier | Dépannage | Peugeot |
| Tussier | Dépannage | Citroën |
| Martin | Électricité | Citroën |
| Martin | Électricité | Renault |
| Martin | Mécanique | Citron |
| Piquard | Mécanique | Renault |
| Piquard | Carrosserie | Fiat |
| Piquard | Carrosserie | Ford |
| Piquard | Alarme | Fiat |
| Piquard | Alarme | Ford |
| Piquard | Électricité | Fiat |
| Piquard | Électricité | Ford |
Dans la section précédente, nous avons présenté un schéma relationnel qui n'était pas en quatrième forme normale en raison du schéma de relation Intervenir. La table 3.2 propose un exemple de relation correspondant à ce schéma de relation. Cette table permet d'observer le phénomène de redondance consécutif au fait que cette table n'est pas en quatrième forme normale. Dans cette table, le nombre de lignes commençant par un nom d'employé donné doit être égal au nombre d'interventions que cet employé peut faire multiplié par le nombre de marques sur lesquelles il peut travailler. Imaginons que l'employé Piquard puisse maintenant travailler sur des voitures de la marque Citroën (on désire ajouter une information dans la base), il faudra alors ajouter trois lignes à la table : une pour chaque type d'intervention (Carrosserie, Alarme et Électricité).
Pour normaliser la relation Intervenir, il faut la décomposer pour aboutir au schéma relationnel suivant :
- Employé(Nom-Employé)
- Intervention(Type-Intervetion)
- Constructeur(Marque)
- Être capable-de(Nom-Employé, Type-Intervetion)
- Etre capable d'intervenir-sur(Nom-Employé, Marque)
3-2-6-c. Dépendance de jointure (DJ)▲
Jusqu'ici, nous avons pu résoudre une redondance dans une relation en la remplaçant par deux de ses projections. Il existe cependant des relations qui ne peuvent pas être décomposées sans perte d'information en deux projections, mais qui peuvent l'être en trois ou plus (ces cas sont assez rares en pratique). C'est ce que permet la normalisation en cinquième forme normale.
Les dépendances de jointures font appel à des notions (projection et jointure) qui seront définies plus loin (cf. section 3.3Algèbre relationnelle).
Définition 23 -dépendance de jointure (DJ)- Soit X1, X2,… Xn des sous-ensembles d'un schéma de relation R. Il y a une dépendance de jointure, notée *{X1, X2,… Xn} dans la relation R, si :
| R=Π (X1)R ▷◁ Π (X2)R ▷◁ … ▷◁ Π (Xn)R |
Définition 24 -dépendance de jointure triviale- Une dépendance de jointure est triviale si une des parties, Xi, est l'ensemble de tous les attributs de R.
3-2-6-d. Cinquième forme normale (5FN)▲
Définition 25 -cinquième forme normale (5FN)- Une relation R est en cinquième forme normale (5FN) si, pour toute dépendance de jointure non triviale *{X1, X2,… Xn} dans R, chacun des Xi contient une clé candidate de R.
En d'autres termes, les seules décompositions qui préservent le contenu sont celles où chacune des tables de la décomposition contient une clé candidate de la table. Il est donc superflu de décomposer de ce point de vue.
Cette forme normale est finale vis-à-vis de la projection et de la jointure : elle garantit qu'une relation en cinquième forme normale ne contient aucune anomalie pouvant être supprimée en effectuant des projections (i.e. des décompositions).
| Relation Fournisseur | ||
|---|---|---|
| Num-Fournisseur | Num-Article | Num-Organisme |
| f1 | a2 | o1 |
| f1 | a1 | o2 |
| f2 | a1 | o1 |
| f1 | a1 | o1 |
Prenons, comme illustration(7), la relation Fournisseur(table 3.3) qui décrit les fournisseurs des organismes de la fonction publique.
La fonction publique a des règles très particulières concernant les fournisseurs pour réduire le potentiel de conflit d'intérêts. Un fournisseur fournit un certain nombre d'articles (par exemple f1 fournit a1 et a2). Le même article peut être fourni par plusieurs fournisseurs (par exemple a1 est fourni par f1 et f2). Un fournisseur peut être attitré à plusieurs organismes (par exemple f1 est attitré à o1 et o2). Un organisme peut avoir plusieurs fournisseurs (par exemple o1 est servi par f1 et f2). Un organisme peut utiliser plusieurs articles (c'est-à-dire que o1 utilise a1 et a2) et un article peut être utilisé par plusieurs organismes (c'est-à-dire que a1 est utilisé par o1 et o2). La règle de la fonction publique est la suivante :
- si un fournisseur fournit un certain article (comme f1 fournit a1),
- le fournisseur est attitré à l'organisme (comme f1 est attitré à o1), et
- l'organisme utilise un article (comme o1 utilise a1),
- alors nécessairement, le fournisseur fournit l'article à l'organisme (f1 fournit a1 à o1).
Le dernier fait est déductible des trois autres.
Cette table contient de la redondance de données parce que certains faits sont répétés. Par exemple, le fait que f1 fournit a1 est répété à deux reprises, une fois parce qu'il fournit a1 à o1 et une autre fois parce qu'il fournit a1 à o2. Le fait que f1 est attitré à o1 est aussi répété à deux reprises. Il en est de même pour o1 qui utilise a1.
La relation Fournisseur souffre d'une dépendance de jointure :
*{(Num-Fournisseur, Num-Article), (Num-Fournisseur, Num-Organisme), (Num-Article, Num-Organisme)}.
Pour résoudre le problème de redondance, il faut décomposer la relation en trois (cf. table 3.4).
| Relation FournisseurArticle | Relation FournisseurOrganisme | Relation ArticleOrganisme | |||||
| Num-Fournisseur | Num-Article | Num-Fournisseur | Num-Organisme | Num-Article | Num-Organisme | ||
| f1 | a2 | f1 | o1 | a2 | o1 | ||
| f1 | a1 | f1 | o2 | a1 | o2 | ||
| f2 | a1 | f2 | o1 | a1 | o1 | ||
Il est important de se convaincre qu'aucune décomposition binaire de cette relation ne préserve le contenu de la relation initiale. Pour cela, il suffit de tenter de joindre deux tables parmi les trois précédentes. Aucune de ces jointures ne produit la relation Fournisseur.
3-2-7. Remarques au sujet de la normalisation▲
Il existe d'autres formes normales comme la forme normale domaine-clé (FNDC), la forme normale de restriction-union ou la sixième forme normale (6NF).
Bien que l'objectif de la normalisation soit d'amener le concepteur à obtenir des relations en forme normale finale (i.e. en cinquième forme normale), cet objectif ne doit pas être interprété comme une loi. Il peut exister, très occasionnellement, de bonnes raisons pour passer outre les principes de la normalisation. De plus, un schéma en cinquième forme normale n'est pas nécessairement un schéma pleinement satisfaisant. D'autres facteurs sont à considérer dans le processus de conception d'une base de données et l'expérience et l'intuition jouent un rôle important.
3-3. Algèbre relationnelle▲
3-3-1. Introduction▲
L'algèbre relationnelle est un support mathématique cohérent sur lequel repose le modèle relationnel. L'objet de cette section est d'aborder l'algèbre relationnelle dans le but de décrire les opérations qu'il est possible d'appliquer sur des relations pour produire de nouvelles relations. L'approche suivie est donc plus opérationnelle que mathématique.
On peut distinguer trois familles d'opérateurs relationnels :
Les opérateurs unaires (Sélection, Projection) :
- ce sont les opérateurs les plus simples, ils permettent de produire une nouvelle table à partir d'une autre table.
Les opérateurs binaires ensemblistes (Union, Intersection Différence) :
- ces opérateurs permettent de produire une nouvelle relation à partir de deux relations de même degré et de même domaine.
Les opérateurs binaires ou n-aires (Produit cartésien, Jointure, Division) :
- ils permettent de produire une nouvelle table à partir de deux ou plusieurs autres tables.
Les notations ne sont pas standardisées en algèbre relationnelle. Ce cours utilise des notations courantes, mais donc pas forcément universelles.
3-3-2. Sélection▲
Définition 26 -sélection- La sélection (parfois appelée restriction) génère une relation regroupant exclusivement toutes les occurrences de la relation R qui satisfont l'expression logique E, on la note σ(E)R.
Il s'agit d'une opération unaire essentielle dont la signature est :
| relation × expression logique → relation |
En d'autres termes, la sélection permet de choisir (i.e. sélectionner) des lignes dans le tableau. Le résultat de la sélection est donc une nouvelle relation qui a les mêmes attributs que R. Si R est vide (i.e. ne contient aucune occurrence), la relation qui résulte de la sélection est vide.
Le tableau 3.6 montre un exemple de sélection.
| Numéro | Nom | Prénom |
|---|---|---|
| 5 | Durand | Caroline |
| 1 | Germain | Stan |
| 12 | Dupont | Lisa |
| 3 | Germain | Rose-Marie |
| Numéro | Nom | Prénom |
|---|---|---|
| 5 | Durand | Caroline |
| 12 | Dupont | Lisa |
3-3-3. Projection▲
Définition 27 -projection- La projection consiste à supprimer les attributs autres que A1,… An d'une relation et à éliminer les n-uplets en double apparaissant dans la nouvelle relation ; on la note Π(A1… An)R.
Il s'agit d'une opération unaire essentielle dont la signature est :
| relation × liste d'attributs → relation |
En d'autres termes, la projection permet de choisir des colonnes dans le tableau. Si R est vide, la relation qui résulte de la projection est vide, mais pas forcément équivalente (elle contient généralement moins d'attributs).
Le tableau 3.7 montre un exemple de sélection.
| Nom |
|---|
| Durand |
| Germain |
| Dupont |
3-3-4. Union▲
Définition 28 -union- L'union est une opération portant sur deux relations R1 et R2 ayant le même schéma et construisant une troisième relation constituée des n-uplets appartenant à chacune des deux relations R1 et R2 sans doublon, on la note R1 ∪ R2.
Il s'agit une opération binaire ensembliste commutative essentielle dont la signature est :
| relation × relation → relation |
Comme nous l'avons déjà dit, R1 et R2 doivent avoir les mêmes attributs et si une même occurrence existe dans R1 et R2, elle n'apparaît qu'une seule fois dans le résultat de l'union. Le résultat de l'union est une nouvelle relation qui a les mêmes attributs que R1 et R2. Si R1 et R2 sont vides, la relation qui résulte de l'union est vide. Si R1 (respectivement R2) est vide, la relation qui résulte de l'union est identique à R2 (respectivement R1).
Le tableau 3.8 montre un exemple d'union.
| Relation R1 | Relation R2 | Relation R | |||||
|---|---|---|---|---|---|---|---|
| Nom | Prénom | Nom | Prénom | Nom | Prénom | ||
| Durand | Caroline | Dupont | Lisa | Durand | Caroline | ||
| Germain | Stan | Juny | Carole | Germain | Stan | ||
| Dupont | Lisa | Fourt | Lisa | Dupont | Lisa | ||
| Germain | Rose-Marie | Germain | Rose-Marie | ||||
| Juny | Carole | ||||||
| Fourt | Lisa | ||||||
3-3-5. Intersection▲
Définition 29 -intersection- L'intersection est une opération portant sur deux relations R1 et R2 ayant le même schéma et construisant une troisième relation dont les n-uplets sont constitués de ceux appartenant aux deux relations, on la note R1 ∩ R2.
Il s'agit une opération binaire ensembliste commutative dont la signature est :
| relation × relation → relation |
Comme nous l'avons déjà dit, R1 et R2 doivent avoir les mêmes attributs. Le résultat de l'intersection est une nouvelle relation qui a les mêmes attributs que R1 et R2. Si R1 ou R2 ou les deux sont vides, la relation qui résulte de l'intersection est vide.
Le tableau 3.9 montre un exemple d'intersection.
| Relation R1 | Relation R2 | Relation R | |||||
|---|---|---|---|---|---|---|---|
| Nom | Prénom | Nom | Prénom | Nom | Prénom | ||
| Durand | Caroline | Dupont | Lisa | Durand | Caroline | ||
| Germain | Stan | Juny | Carole | Dupont | Lisa | ||
| Dupont | Lisa | Fourt | Lisa | Juny | Carole | ||
| Germain | Rose-Marie | Durand | Caroline | ||||
| Juny | Carole | ||||||
3-3-6. Différence▲
Définition 30 -différence- La différence est une opération portant sur deux relations R1 et R2 ayant le même schéma et construisant une troisième relation dont les n-uplets sont constitués de ceux ne se trouvant que dans la relation R1 ; on la note R1 − R2.
Il s'agit une opération binaire ensembliste non commutative essentielle dont la signature est :
| relation × relation → relation |
Comme nous l'avons déjà dit, R1 et R2 doivent avoir les mêmes attributs. Le résultat de la différence est une nouvelle relation qui a les mêmes attributs que R1 et R2. Si R1 est vide, la relation qui résulte de la différence est vide. Si R2 est vide, la relation qui résulte de la différence est identique à R1.
Le tableau 3.10 montre un exemple de différence.
| Relation R1 | Relation R2 | Relation R | |||||
|---|---|---|---|---|---|---|---|
| Nom | Prénom | Nom | Prénom | Nom | Prénom | ||
| Durand | Caroline | Dupont | Lisa | Germain | Stan | ||
| Germain | Stan | Juny | Carole | Germain | Rose-Marie | ||
| Dupont | Lisa | Fourt | Lisa | ||||
| Germain | Rose-Marie | Durand | Caroline | ||||
| Juny | Carole | ||||||
3-3-7. Produit cartésien▲
Définition 31 -produit cartésien- Le produit cartésien est une opération portant sur deux relations R1 et R2 et qui construit une troisième relation regroupant exclusivement toutes les possibilités de combinaison des occurrences des relations R1 et R2, on la note R1 × R2.
Il s'agit une opération binaire commutative essentielle dont la signature est :
| relation × relation → relation |
Le résultat du produit cartésien est une nouvelle relation qui a tous les attributs de R1 et tous ceux de R2. Si R1 ou R2 ou les deux sont vides, la relation qui résulte du produit cartésien est vide. Le nombre d'occurrences de la relation qui résulte du produit cartésien est le nombre d'occurrences de R1 multiplié par le nombre d'occurrences de R2.
Le tableau 3.11 montre un exemple de produit cartésien.
| Relation Amie | Relation Cadeau | Relation R | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Nom | Prénom | Article | Prix | Nom | Prénom | Article | Prix | ||
| Fourt | Lisa | livre | 45 | Fourt | Lisa | livre | 45 | ||
| Juny | Carole | poupée | 25 | Fourt | Lisa | poupée | 25 | ||
| montre | 87 | Fourt | Lisa | montre | 87 | ||||
| Juny | Carole | livre | 45 | ||||||
| Juny | Carole | poupée | 25 | ||||||
| Juny | Carole | montre | 87 | ||||||
3-3-8. Jointure, thêta-jointure, équijointure, jointure naturelle▲
3-3-8-a. Jointure▲
Définition 32 -jointure- La jointure est une opération portant sur deux relations R1 et R2 qui construit une troisième relation regroupant exclusivement toutes les possibilités de combinaison des occurrences des relations R1 et R2 qui satisfont l'expression logique E. La jointure est notée R1 ▷◁ER2.
Il s'agit d'une opération binaire commutative dont la signature est :
| relation × relation × expression logique → relation |
Si R1 ou R2 ou les deux sont vides, la relation qui résulte de la jointure est vide.
En fait, la jointure n'est rien d'autre qu'un produit cartésien suivi d'une sélection :
| R1 ▷◁E R2 = σE (R1 × R2) |
Le tableau 3.12 montre un exemple de jointure.
| Relation Famille | Relation Cadeau | Relation R | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom | Prénom | Age | AgeC | Article | Prix | Nom | Prénom | Age | AgeC | Article | Prix | ||
| Fourt | Lisa | 6 | 99 | livre | 30 | Fourt | Lisa | 6 | 99 | livre | 45 | ||
| Juny | Carole | 42 | 6 | poupée | 60 | Fourt | Lisa | 6 | 20 | poupée | 25 | ||
| Fidus | Laure | 16 | 20 | baladeur | 45 | Fourt | Lisa | 6 | 10 | montre | 87 | ||
| 10 | déguisement | 15 | Juny | Carole | 42 | 99 | livre | 45 | |||||
| Fidus | Laure | 16 | 99 | poupée | 25 | ||||||||
| Fidus | Laure | 16 | 20 | montre | 87 | ||||||||
3-3-8-b. Thêta-jointure▲
Définition 33 -thêta-jointure- Une thêta-jointure est une jointure dans laquelle l'expression logique E est une simple comparaison entre un attribut A1 de la relation R1 et un attribut A2 de la relation R2. La thêta-jointure est notée R1 ▷◁ER2.
3-3-8-c. Équijointure▲
Définition 34 -équijointure- Une équijointure est une thêta-jointure dans laquelle l'expression logique E est un test d'égalité entre un attribut A1 de la relation R1 et un attribut A2 de la relation R2. L'équijointure est notée R1 ▷◁A1,A2R2.
Il vaut mieux écrire R1 ▷◁A1=A2 R2 que R1 ▷◁A1,A2 R2, car cette dernière notation peut prêter à confusion avec une jointure naturelle explicite.
3-3-8-d. Jointure naturelle▲
Définition 35 -jointure naturelle- Une jointure naturelle est une jointure dans laquelle l'expression logique E est un test d'égalité entre les attributs qui portent le même nom dans les relations R1 et R2. Dans la relation construite, ces attributs ne sont pas dupliqués, mais fusionnés en une seule colonne par couple d'attributs. La jointure naturelle est notée R1 ▷◁ R2. On peut préciser explicitement les attributs communs à R1 et R2 sur lesquels porte la jointure : R1 ▷◁A1,… AnR2.
Généralement, R1 et R2 n'ont qu'un attribut en commun. Dans ce cas, une jointure naturelle est équivalente à une équijointure dans laquelle l'attribut de R1 et celui de R2 sont justement les deux attributs qui portent le même nom.
Lorsque l'on désire effectuer une jointure naturelle entre R1 et R2 sur un attribut A1 commun à R1 et R2, il vaut mieux écrire R1 ▷◁A1 R2 que R1 ▷◁ R2. En effet, si R1 et R2 possèdent deux attributs portant un nom commun, A1 et A2, R1 ▷◁A1 R2 est bien une jointure naturelle sur l'attribut A1, mais R1 ▷◁ R2 est une jointure naturelle sur le couple d'attributs A1, A2, ce qui produit un résultat très différent !
Le tableau 3.13 montre un exemple de jointure naturelle.
| Relation Famille | Relation Cadeau | Relation R | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom | Prénom | Age | Age | Article | Prix | Nom | Prénom | Age | Article | Prix | ||
| Fourt | Lisa | 6 | 40 | livre | 45 | Fourt | Lisa | 6 | poupée | 25 | ||
| Juny | Carole | 40 | 6 | poupée | 25 | Juny | Carole | 40 | livre | 45 | ||
| Fidus | Laure | 20 | 20 | montre | 87 | Fidus | Laure | 20 | montre | 87 | ||
| Choupy | Emma | 6 | Choupy | Emma | 6 | poupée | 25 | |||||
3-3-9. Division▲
Définition 36 -division- La division est une opération portant sur deux relations R1 et R2, telles que le schéma de R2 est strictement inclus dans celui de R1, qui génère une troisième relation regroupant toutes les parties d'occurrences de la relation R1 qui sont associées à toutes les occurrences de la relation R2 ; on la note R1 ÷ R2.
Il s'agit d'une opération binaire non commutative dont la signature est :
| relation × relation → relation |
Autrement dit, la division de R1 par R2 (R1 ÷ R2) génère une relation qui regroupe tous les n-uplets qui, concaténés à chacun des n-uplets de R2, donnent toujours un n-uplet de R1.
La relation R2 ne peut pas être vide. Tous les attributs de R2 doivent être présents dans R1 et R1 doit posséder au moins un attribut de plus que R2 (inclusion stricte). Le résultat de la division est une nouvelle relation qui a tous les attributs de R1 sans aucun de ceux de R2. Si R1 est vide, la relation qui résulte de la division est vide.
Le tableau 3.14 montre un exemple de division.
| Relation Enseignant | Relation Étudiant | Relation R | |||
|---|---|---|---|---|---|
| Enseignant | Étudiant | Nom | Enseignant | ||
| Germain | Dubois | Dubois | Germain | ||
| Fidus | Pascal | Pascal | Fidus | ||
| Robert | Dubois | ||||
| Germain | Pascal | ||||
| Fidus | Dubois | ||||
| Germain | Durand | ||||
| Robert | Durand | ||||


